Domande per Esame

Formule Utili

Nome	Formula	Note
Sintesi RM	$s(t)=c(t)\cdot m(t)$
Sintesi AM	$s(t)=c(t)+c(t)\cdot m(t)$	$m(t)$ deve avere come codominio $[0,1]$
Sintesi FM	$s(t)=A\cdot sin(2\pi f_{c}t+I\cdot sin(2\pi f_{m}t))$

Teoria

Aliasing

Si consideri un sistema audio digitale con frequenza di campionamento fissata a 48000 Hz. Un’onda a dente di sega con frequenza fondamentale a 5000 Hz e ampiezza di picco pari a -6 dB produrrà aliasing percepibile? La situazione cambierebbe se sostituissi l’onda a dente di sega con un’onda sinusoidale? Motivare la risposta.

Secondo il teorema di Nyquist è possibile campionare qualunque segnale a frequenza $f_c$ senza aliasing utilizzando un campionatore a frequenza $f=2\cdot f_c$. per cui un sistema di campionamento con frequenza fissata a 48kHz può campionare un segnale con frequenza fino a 24kHz senza produrre aliasing.

Un segnale a 5kHz, a prescindere dal suo inviluppo, non genererà aliasing utilizzando un campionatore a 48kHz.

Considerare un sistema audio digitale con frequenza di campionamento di 44100 Hz. Per ciascuno dei seguenti segnali, descrivere brevemente la qualità della rappresentazione del suo spettro motivando le risposte:

1. Segnale sinusoidale con fondamentale a 3000 Hz.
2. Segnale sinusoidale con fondamentale a 30000 Hz.
3. Segnale sinusoidale con fondamentale a 60000 Hz.
4. Segnale a dente di sega con fondamentale a 4410 Hz.
5. Segnale a dente di sega con fondamentale a 5000 Hz.
6. Segnale ottenuto tramite sintesi per modulazione di frequenza (formulazione “classica” di John Chowning) con portante a 10000 Hz, modulante a 5000 Hz, indice di modulazione 1.

Secondo il teorema di Nyquist è possibile campionare qualunque segnale a frequenza $f_c$ senza aliasing utilizzando un campionatore a frequenza $f=2\cdot f_c$. per cui un sistema di campionamento con frequenza fissata a 44kHz può campionare un segnale con frequenza fino a 22kHz senza produrre aliasing, a priori dall’inviluppo del segnale.

1. Il segnale è al di sotto dei 22kHz e quindi il processo di campionamento non produce aliasing.
2. Il segnale supera i 22kHz e quindi produce aliasing.
3. Il segnale supera i 22kHz e quindi produce aliasing.
4. Il segnale ha una fondamentale al di sotto dei 22kHz, tuttavia ha anche infinite armoniche dispari a frequenza $f_i=4410\cdot i$, $\forall i\in \mathbb{N},i\mathrm{mod}2=1$. Per evitare gli effetti di aliasing sarebbe necessario utilizzare un filtro che taglia tutte le armoniche maggiori di 22kHz.
5. Come risposta 4.
6. Un segnale di chowning con indice di modulazione i ha $2\cdot (i+2)+1$ frequenze con contenuto in ampiezza non nullo. Lo spettro del segnale è pari a $f_c\pm k\cdot f_m$, dove $k\in [0,i+2]$.
   Quindi gli estremi della banda saranno $10kHz-3\cdot 5kHz=-5kHz$ e $10kHz+3\cdot 5kHz=25kHz$.
   Non solo la banda supera i 22kHz come limite massimo, ma si ha un ribaltamento del segnale per le frequenze negative.

Campionamento E Quantizzazione

Si consideri un sistema audio PCM con rappresentazione intera a 32 bit.
Cerco di riprodurre un segnale sinusoidale con ampiezza di picco di -150 dB. Cosa succede? Se il sistema avesse rappresentazione floating point a 32 bit, cosa cambierebbe?

In un sistema di rappresentazione binario lineare ogni bit permette di rappresentare circa 6dB, per cui con 32 bit si possono rappresentare circa $32bit\ast 6\frac{dB}{bit}=192dB$ Full Scale (ovvero il cui massimo è 0dB e minimo -192dB). Dunque è possibile rappresentare il segnale con ampiezza di picco -150dB, la sua dinamica sarà (-192, -150], ovvero di soli 42dB.

Usando una rappresentazione floating point si migliora di molto la precisione della rappresentazione del segnale.

Qual è la frequenza di un suono con un periodo di 20 ms? Motivare la risposta.
Qual è il periodo di un suono con frequenza di 2000 Hz? Motivare la risposta.

La relazione che lega frequenza e periodo è $f=\frac{1}{T}$, ovvero sono inversamente proporzionali.
Applicando questa formula alla richiesta la frequenza di un suono con periodo di 20ms è $f=\frac{1}{20\cdot 10^{-3}s}=50Hz$, mentre il periodo di un suono con frequenza 2000Hz è $T=\frac{1}{2000Hz}=5\cdot 10^{-4}s=0.5ms$.

Qual è la frequenza di un suono con un periodo di 4 ms? Motivare la risposta.
Qual è il periodo di un suono con frequenza di 2000 Hz? Motivare la risposta.

La relazione che lega frequenza e periodo è $f=\frac{1}{T}$, ovvero sono inversamente proporzionali.
Applicando questa formula alla richiesta la frequenza di un suono con periodo di 4ms è $f=\frac{1}{4\cdot 10^{-3}s}=250Hz$, mentre il periodo di un suono con frequenza 2000Hz è $T=\frac{1}{2000Hz}=5\cdot 10^{-4}s=0.5ms$.

Qual è la minima ampiezza riproducibile in un sistema audio digitale a rappresentazione intera con risoluzione di 24 bit? Cosa succede se cerco di riprodurre un’onda sinusoidale a tale ampiezza minima?

La minima ampiezza riproducibile in qualunque sistema di rappresentazione audio digitale lineare è quella del singolo bit, che contribuisce a circa 6dB. Tuttavia riprodurre un’onda che sfrutta un solo bit di risoluzione (a fronte del full scale del quantizzatore) porta a fenomeni di low quality quantization noise, visto che il sistema di rappresentazione potrà rappresentare soltanto i picchi massimi e minimi e non buona parte dei valori di mezzo del segnale.

Inoltre, sempre a causa dello stesso motivo, l’onda quantizzata risulterà essere un’onda quadra.

E corretto dire che un campione audio PCM contiene una rappresentazione del contenuto frequenziale del suono? Motivare la risposta.

Il campione audio PCM è l’unità più piccola risultato del processo di quantizzazione e campionamento di un segnale audio. Durante la fase di campionamento il segnale audio viene discretizzato in campioni generalmente equidistanti, mentre durante la fase di quantizzazione viene discretizzata l’ampiezza del segnale nell’istante di tempo a cui fa riferimento il campione.

Quindi no, dire che il campione PCM contiene un rappresentazione del contenuto frequenziale del suono è errato in quanto contiene una rappresentazione del contenuto di ampiezza del suono nello specifico istante a cui fa riferimento il campione.

Filtri

Si consideri un segnale sinusoidale con frequenza fondamentale di 4000 Hz e ampiezza di -6 dBfs, a cui viene applicato un filtro passa-alto di secondo ordine con frequenza di taglio di 8000 Hz.
Disegnare lo spettrogramma del segnale risultante, con le appropriate unità di misura sugli assi, o descrivere dettagliatamente il suo spettro.

Un filtro di ordine n applica un’attenuazione di $6n$ dB per ottava al di fuori della sua banda di passaggio. Ricordando che un’ottava è l’intervallo in frequenza che corrisponde al raddoppiamento (o dimezzamento) della frequenza, si ha che un filtro passa alto di secondo ordine, con frequenza di taglio di 8kHz attenuerà il segnale di -12dB a 4kHz.

Il segnale sinusoidale finale avrà solamente un contenuto in frequenza pari a -18dBFS a 4kHz, ovvero sarà attenuato di 12dB.

Qual è la definizione di ordine di un filtro? (Suggerimento: non è la sua attenuazione per ottava!)
In cosa differisce un filtro a risposta finita da uno a risposta infinita?

Si può analizzare la definizione di un ordine di filtro da due punti divista, quello pratico e quello matematico.

• A livello pratico l’ordine di un filtro è dato dal numero di campioni di ritardo $n$ della linea usata per realizzare il filtro.
• A livello matematico, invece, l’ordine del filtro è dal numero di punti di singolarità che presenta la funzione di trasferimento del filtro, ovvero il numero di zeri e poli.

La stessa analisi si può fare per la differenza tra tipi di filtri:

• A livello pratico la differenza tra FIR e IIR è che durante la progettazione dei primi non si utilizzano linee di feedback, mentre nei secondi si.
• A livello matematico si analizza invece la risposta all’impulso della funzione di trasferimento del filtro, ovvero il prodotto tra la funzione di trasferimento e una delta di Dirac. Se il risultato diverge verso l’infinito allora si ha un filtro IIR, altrimenti si ha un filtro FIR.

Considerare un segnale sinusoidale con frequenza fondamentale di 500 Hz e ampiezza di -10 dBfs.
Applico a tale segnale un filtro passa-basso di secondo ordine con frequenza di taglio di 1000 Hz. Quale sarà lo spettro del segnale risultante? Quale la sua ampiezza? Motivare la risposta.

Un filtro di ordine n applica un’attenuazione di $6\cdot n$ dB per ottava, dove un’ottava è definita come la frequenza $f_1$ tale per cui si ha un rapporto 2:1 (o 1:2) rispetto alla frequenza $f$.

Per cui un filtro passa basso di secondo ordine con frequenza di taglio a 1000Hz presenterà un’attenuazione di -12dB a 2000Hz, ma essendo un filtro passa basso non presenta alcuna attenuazione a 500Hz.

Dato che un segnale puramente sinusoidale non ha armoniche, il segnale filtrato rimarrà invariato.

Modulazione

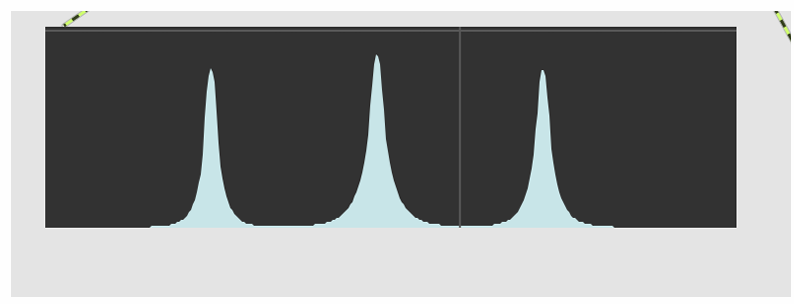
Come posso ottenere uno spettrogramma di questo tipo utilizzando due soli oscillatori sinusoidali? (Non dimenticare che la visualizzazione dello spettrogramma è, in generale, approssimativa)

Per ottenere uno spettrogramma di questo tipo si può utilizzare una tecnica di modulazione in ampiezza, che ha proprio come caratteristica quella di creare uno spettro con tre picchi, uno centrato nella frequenza $f_c$ del segnale originale e gli altri due equidistanti a distanza $f_m$ dal centro.

RMS

Un segnale a onda quadra con frequenza di 100 Hz ha ampiezza normalizzata di picco pari a 0.25.
Qual è la sua ampiezza RMS, considerata su una finestra di 10 ms?
Sostituendo l’onda quadra con un’onda a dente di sega, l’ampiezza RMS rimane costante, aumenta o diminuisce?

L’RMS di un segnale s(t) periodico di periodo T è uguale a $\sqrt{\frac{1}{T}{\Sigma }_0^T{s}^2(t)}$, tuttavia in alcuni casi noti come sinusoidi, onde quadre, onde triangolari ed onde a dente di sega vi sono formule note che permettono di calcolarlo in maniera più rapida a partire dall’ampiezza di picco del segnale, se la finestra di analisi è quella dell’intero periodo. Chiamando $A_p$ l’ampiezza di picco:

• $RM{S}_{sin}=\frac{A_p}{\sqrt{2}}$
• $RM{S}_{tri}=RM{S}_{saw}=\frac{A_p}{\sqrt{3}}$
• $RM{S}_{square}=A_p$

Anche senza usare numeri è facile notare che $\frac{A_p}{\sqrt{3}}<A_p$ per ogni valore di picco positivo.
Applicando al caso richiesto, 10ms corrispondono al periodo per un’onda a frequenza 100Hz, per cui possiamo dire che:

• L’RMS dell’onda quadra è di $0.25$
• L’RMS dell’onda a dente di sega è di $0.144$

Dunque sostituendo l’onda quadra con l’onda a dente di sega l’RMS diminuirebbe.

Quali delle seguenti affermazioni sono corrette?

1. Un campione audio PCM mi permette di conoscere la frequenza di un suono.
2. Un campione audio PCM contiene una rappresentazione dell’ampiezza del suono.
3. Da un singolo campione audio PCM posso stimare l’ampiezza percepita del suono.

1. Falso. Un campione audio PCM salva le informazioni di ampiezza del segnale.
2. Vero.
3. Falso. Per stimare l’ampiezza percepita del suono è bisogno analizzare una finestra del segnale, e in generale la variazione di ampiezza tra i campioni.

Un segnale a onda quadra viene considerato lungo una finestra di un secondo. La sua ampiezza di picco è -6 dBfs; qual è la sua ampiezza RMS?
Consideriamo ora, lungo la stessa finestra, un segnale sinusoidale con la stessa ampiezza di picco: la sua ampiezza RMS è maggiore, uguale o minore rispetto a quella dell’onda quadra?

L’RMS di un segnale s(t) periodico di periodo T è uguale a $\sqrt{\frac{1}{T}{\Sigma }_0^T{s}^2(t)}$, tuttavia in alcuni casi noti come sinusoidi, onde quadre, onde triangolari ed onde a dente di sega vi sono formule note che permettono di calcolarlo in maniera più rapida a partire dall’ampiezza di picco del segnale, se la finestra di analisi è quella dell’intero periodo. Chiamando $A_p$ l’ampiezza di picco:

• $RM{S}_{sin}=\frac{A_p}{\sqrt{2}}$
• $RM{S}_{tri}=RM{S}_{saw}=\frac{A_p}{\sqrt{3}}$
• $RM{S}_{square}=A_p$

Si può notare che nell’intero periodo l’RMS è massimo in onde quadre, in quanto $A_p>\frac{A_p}{k}$, $\forall k\in N$, $k>1$.

Max

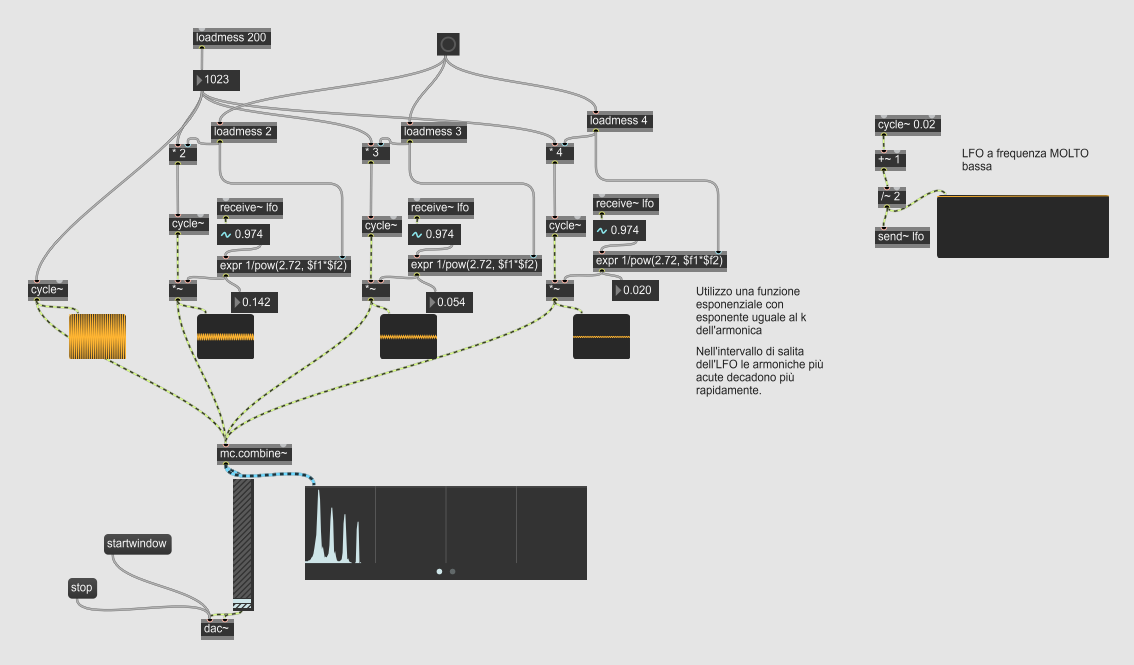
a. Costruire una patch che produca le prime quattro armoniche di un segnale con frequenza fondamentale a 220 Hz. L’ampiezza delle parziali deve complessivamente decrescere con la frequenza.
b. Aggiungere alla patch un sistema di inviluppi di ampiezza, in modo tale che le parziali acute decadano più rapidamente di quelle gravi.

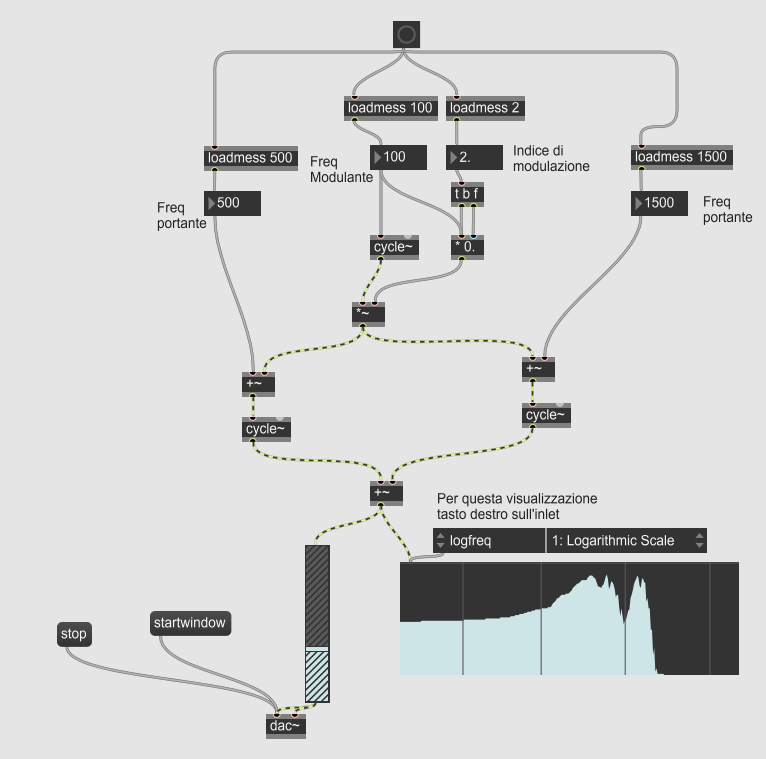
Creare una patch che realizzi un processo di sintesi FM con i seguenti parametri: frequenza modulante a 100 Hz, due portanti con frequenze di 500 e 1500 Hz, indice di modulazione 2 per entrambe le modulanti. Descrivere lo spettro risultante, motivando la risposta.

Nella sintesi FM la banda del segnale è di $f_c \pm kf_m$, dove $f_c$ è la frequenza della portante e $f_m$ della modulante. K invece viene approssimato come $K = I + 2$ dove $I$ è l'indice di modulazione.

Quindi l’aspettativa è che la banda sia grossomodo l’unione di $500Hz\pm 4\cdot 100Hz=[100,900]Hz$ e $1500Hz\pm 4\cdot 100Hz=[1100,1900]Hz$.

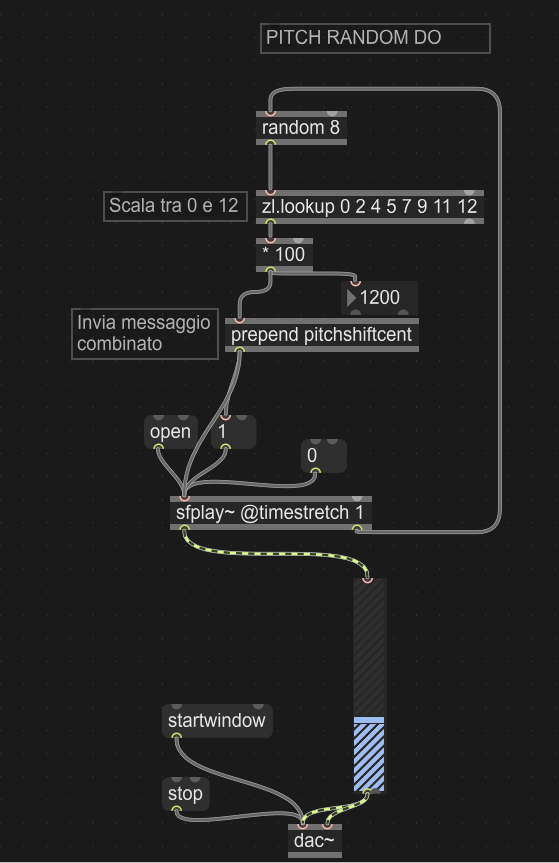
Realizzare un semplice processo che riproduca ripetutamente questo campione audio, ogni volta con una trasposizione diversa scelta a caso nella scala di Do maggiore:
https://www.dropbox.com/s/1ix8uronfdd8cfm/middleC.wav?dl=0

---

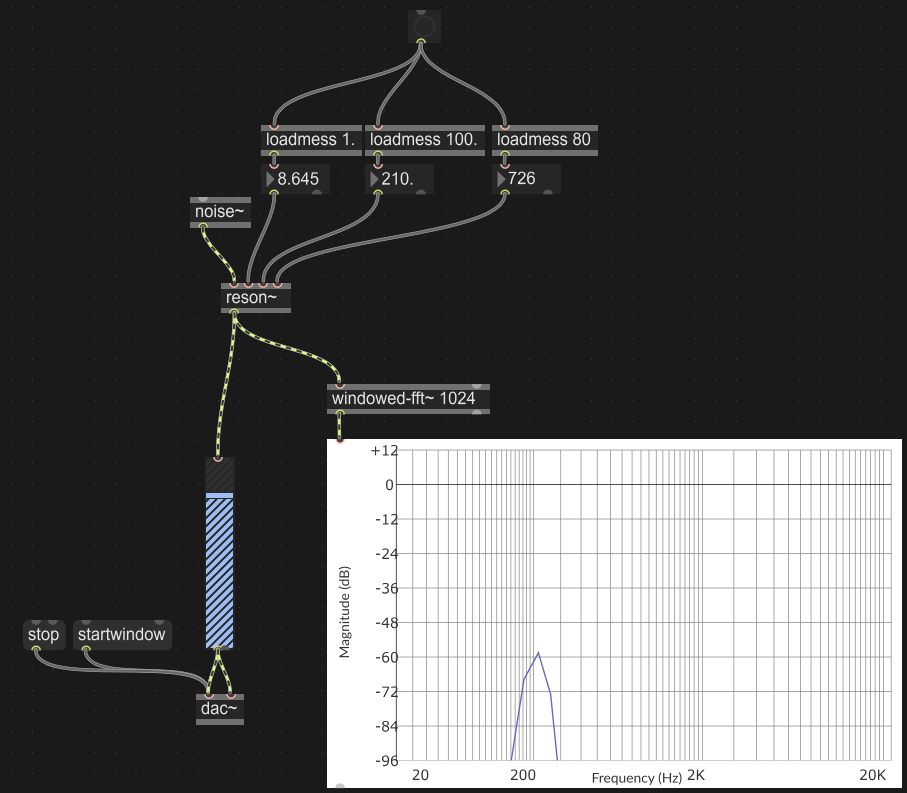
Costruire una patch contenente un generatore di rumore bianco collegato a un filtro risonante a banda stretta, tale che la qualità percepita del segnale risultante sia prossima a quella di una sinusoide leggermente “instabile”.

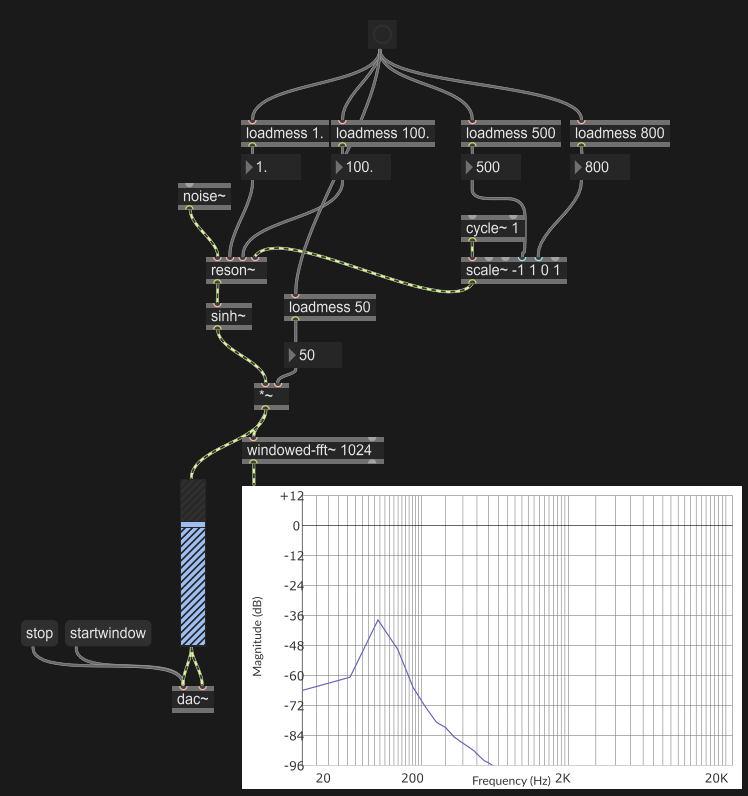
Far dipendere la larghezza di banda del filtro da un LFO, facendo in modo che l’ampiezza del segnale resti approssimativamente costante (e senza usare compressori o limiter!)

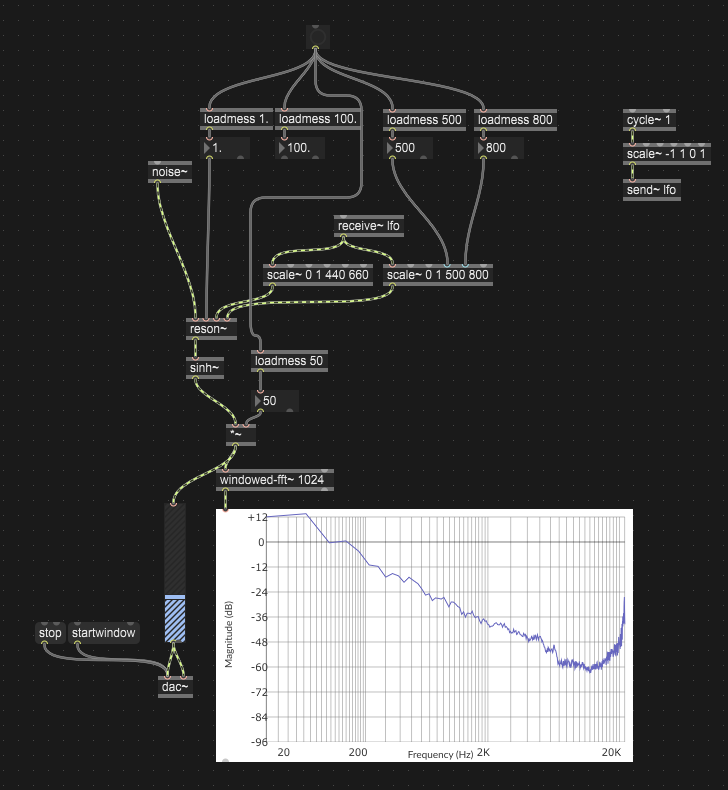
Far dipendere dallo stesso LFO la frequenza di taglio del filtro, che dovrà muoversi lungo un ambito di una quinta giusta.

---

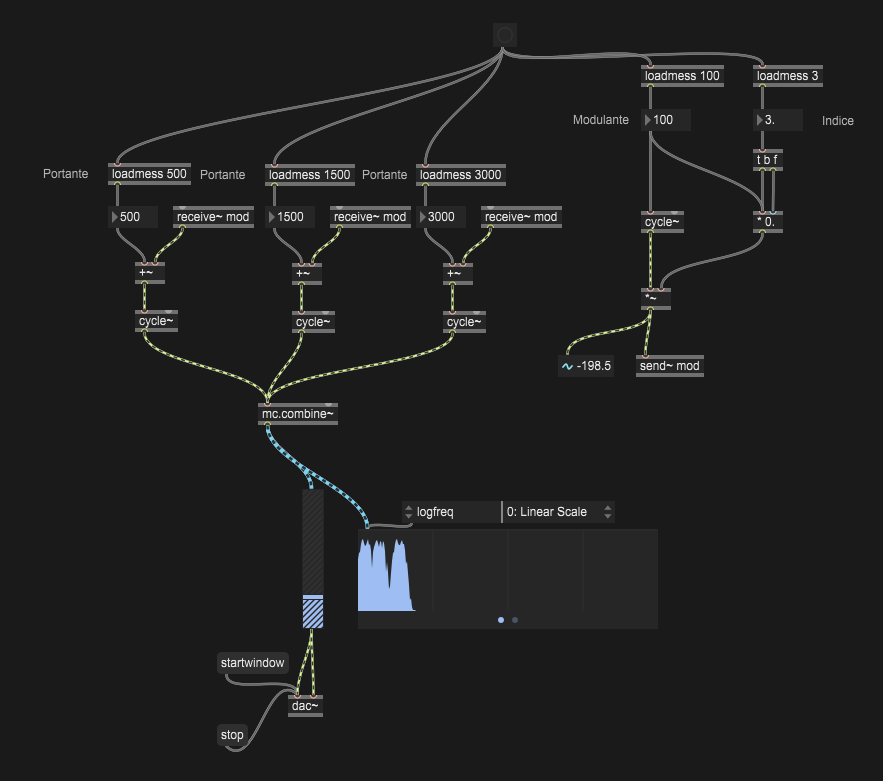
Disegnare un grafico nel dominio della frequenza che rappresenti lo spettro di un suono di sintesi FM con tre portanti rispettivamente a 500, 1500 e 3000 Hz, modulante a 100 Hz e indice di modulazione 3. Descrivere il suono risultante.

Figura successiva

Creare una patch che realizzi il processo di sintesi descritto al punto precedente.

---

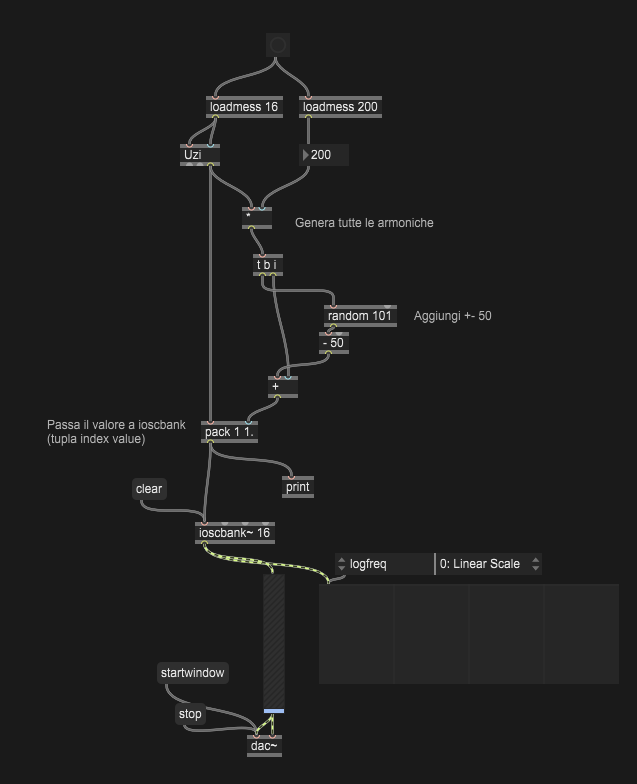
Costruire un sintetizzatore additivo con almeno 16 parziali che produca un suono con struttura approssimativamente (ma non esattamente) armonica.

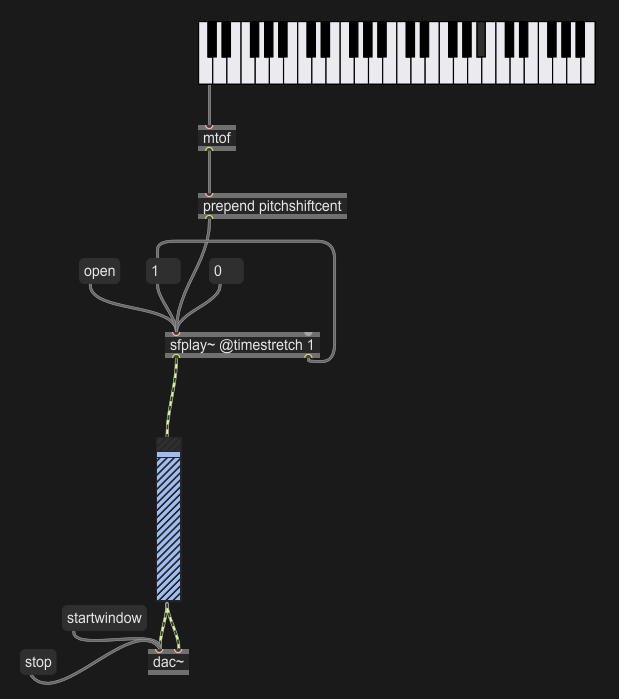
Realizzare un semplice campionatore che riproduca il suono che vi verrà consegnato con una trasposizione indicata in semitoni scelta dall’utente.

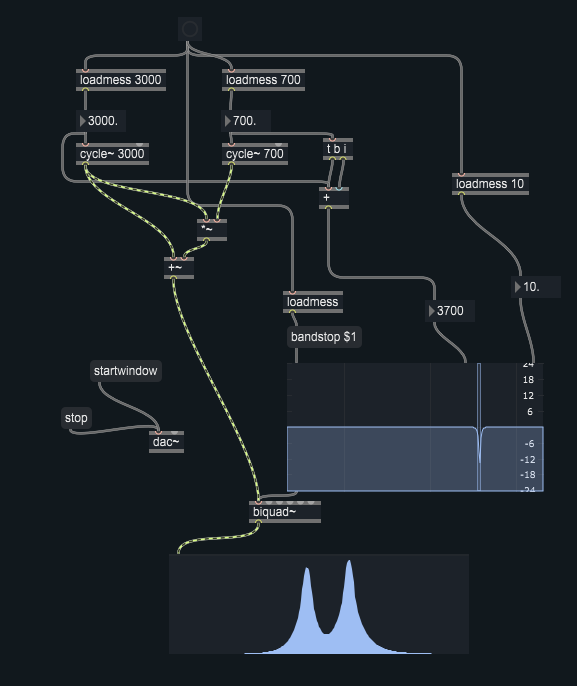
Programmare un patch in modo da filtrare in alternativa una delle due bande laterali di un un suono ottenuto da modulazione d’ampiezza tra un oscillatore sinusioidale con frequenza 3000 Hz ed un secondo oscillatore sinusoidale con frequenza 700 Hz.
Le proprietà del filtro (f taglio, Q) devono essere determinate direttamente a partire dai valori delle frequenze di portante e modulante e possono essere modificate dinamicamente in modo da ricalcolare la frequenza di taglio del filtro al variare di quelle degli oscillatori.

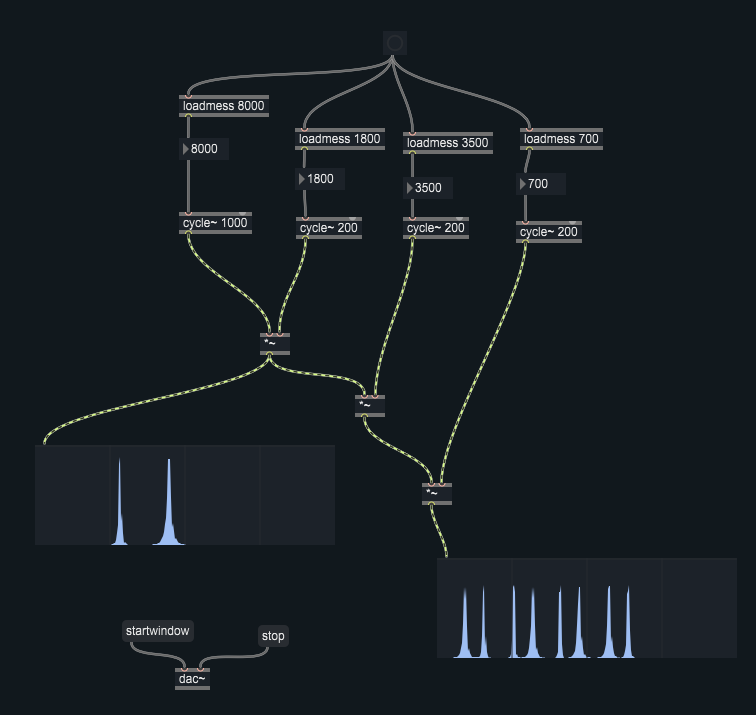
Programmare un patch nel quale viene prodotto un suono a 8 componenti a partire da sinusoidi sfruttando la tecnica della modulazione d’ampiezza (AM) o della modulazione ad anello (RM). Implementare anche una funzione che permetta di calcolare i valori delle frequenze delle 8 componenti

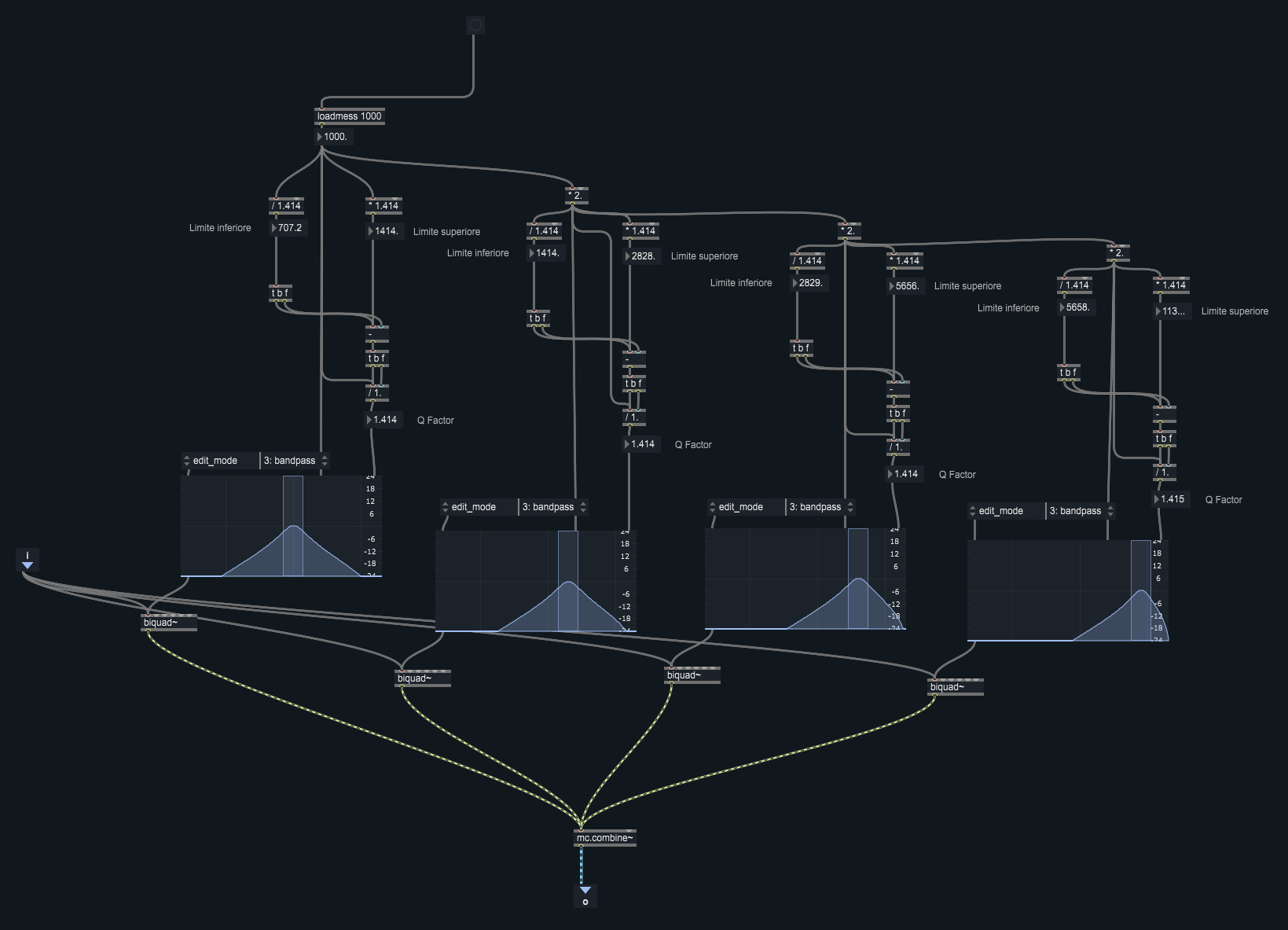
Programmare un patch in modo da calcolare a partire dal valore della frequenza centrale i valori delle frequenze estreme della banda di un filtro passa banda, la cui larghezza corrisponda a circa un’ottava. Calcolare anche il fattore Q.
A partire da questo sistema programmare un banco di 4 filtri passabanda con attenuazione di 12 dB/ottava la cui frequenze centrale sia a rispettiva distanza di 1 ottava