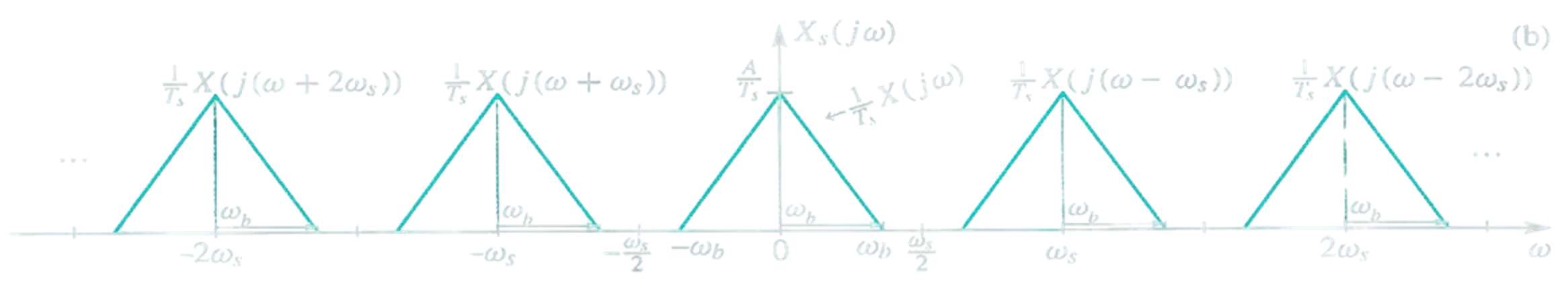In analisi matematica, la Trasformata di Fourier è una trasformata integrale, cioè un operatore che trasforma una funzione in un’altra funzione mediante un’integrazione. Trova numerose applicazioni nella fisica e nell’ingegneria ed è uno degli strumenti matematici maggiormente utilizzati nell’ambito delle scienze pure e applicate, permettendo di scrivere una funzione dipendente dal tempo come combinazione lineare (eventualmente continua) di funzioni di base esponenziali.
La trasformata di Fourier associa a una funzione i valori dei coefficienti di questi sviluppi lineari, dandone in questo modo una rappresentazione nel dominio delle frequenze che viene spesso chiamata spettro della funzione (la relazione con il concetto di spettro di un operatore può essere compresa se si considera l’operatore di convoluzione con la funzione in esame). A volte si intende per trasformata di Fourier la funzione che risulta dall’applicazione di questo operatore.
In termini semplici, la trasformata di Fourier permette di passare da una rappresentazione nel dominio del tempo (o spazio) a una rappresentazione nel dominio delle frequenze. Se abbiamo una funzione che descrive un segnale nel tempo, la sua trasformata di Fourier ci darà una descrizione di quel segnale in termini delle sue frequenze componenti.
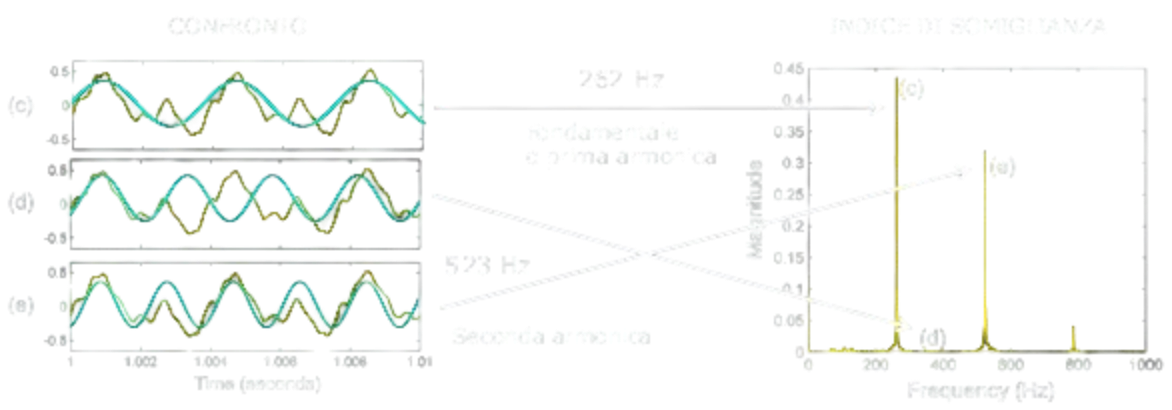
Si può sintetizzare il suono analogico tramite la trasformata inversa, ovvero la sintesi di Fourier.
L’analisi di Fourier si può presentare in diverse modalità in base al tipo di segnale da analizzare.
Tipi di segnale
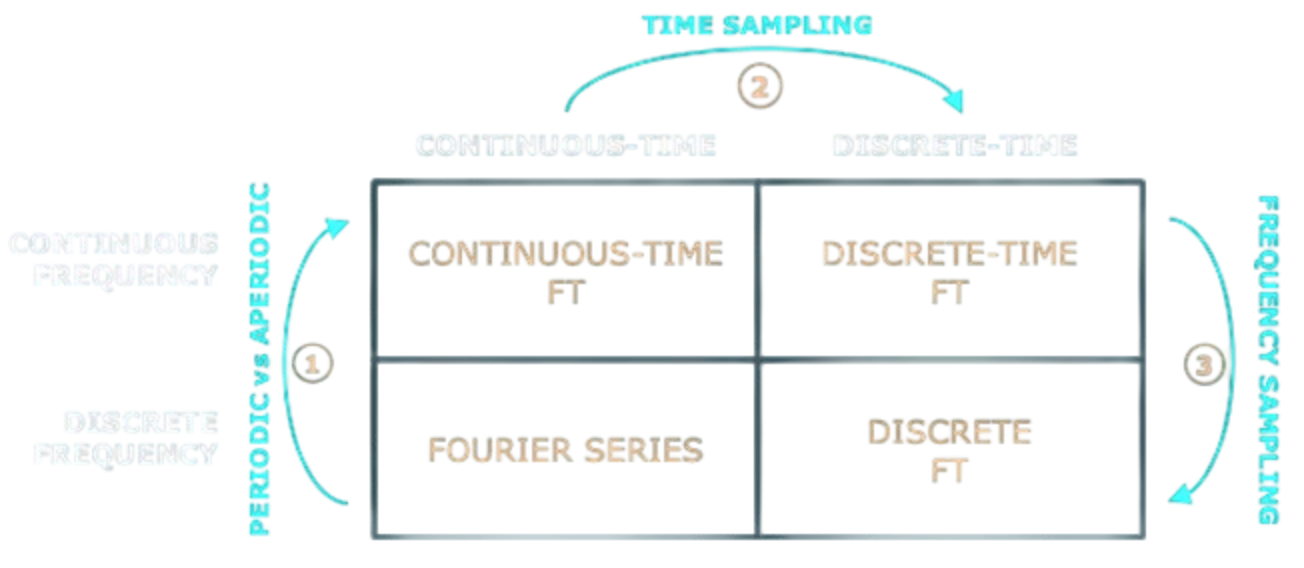
Un segnale può essere continuo o discreto nel tempo.
Quando un segnale è continuo nel tempo, la trasformata di Fourier sarà discreta in frequenza, e viceversa.
Quindi tramite le operazioni di Campionamento e Quantizzazione si ottiene una trasformata di Fourier continua nel tempo.
Serie di Fourier
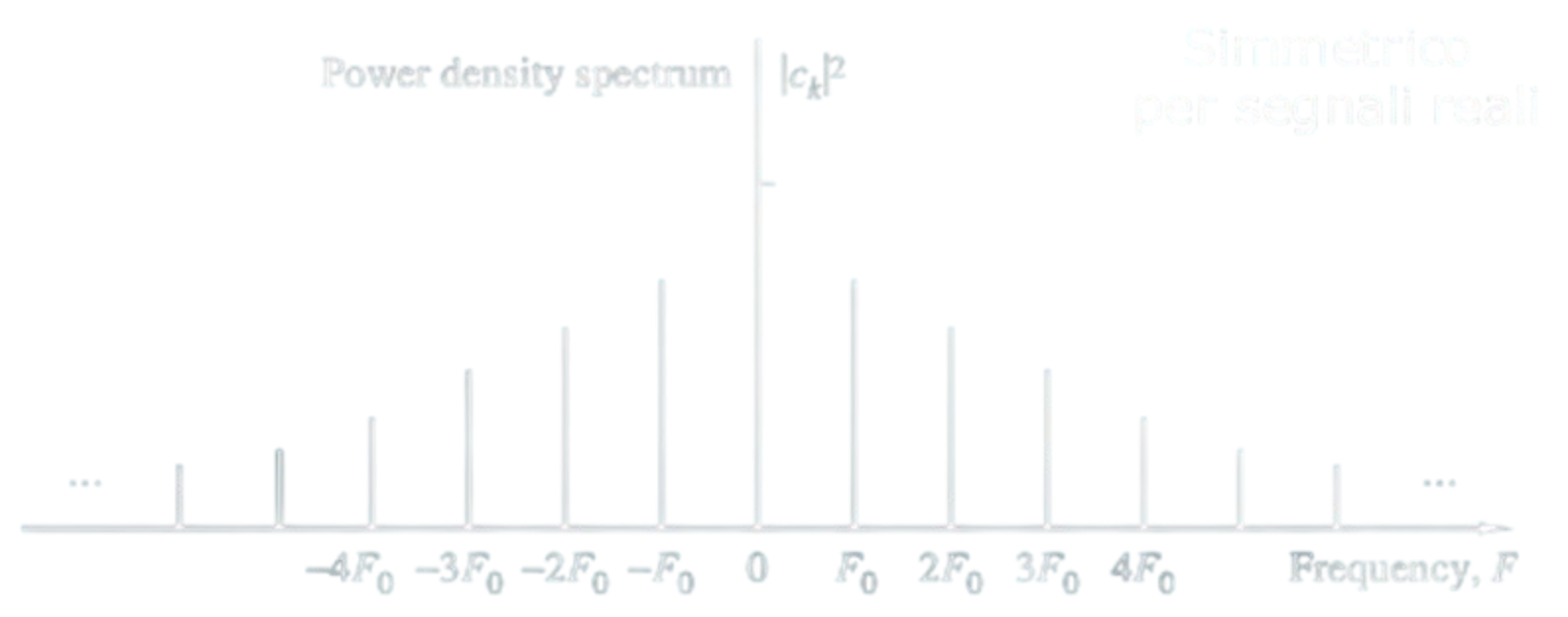
Nel caso di segnali periodici continui si realizza la conversione tempo / frequenza tramite la Serie di Fourier, che descrive un segnale una somma pesata di sinusoidi armoniche, multiple della frequenza principale di un multiplo k intero. Se il coefficiente k non fosse intero il segnale non potrebbe essere periodico.
Il segnale in frequenza è la densità spettrale di potenza, non energia, in quanto l’energia dei segnali periodici è infinita.Link to original
Discrete Time Fourier Transform
Link to originalIn matematica, la trasformata di Fourier a tempo discreto (DTFT) è una forma di analisi di Fourier applicabile a una sequenza di valori discreti.
La DTFT viene spesso utilizzata per analizzare campioni di una funzione continua. Il termine tempo discreto si riferisce al fatto che la trasformata opera su segnali aperiodici a tempo discreto.
dove indica multipli del periodo di campionamento e la frequenza dello spettro è continua.
Discrete Fourier Transform
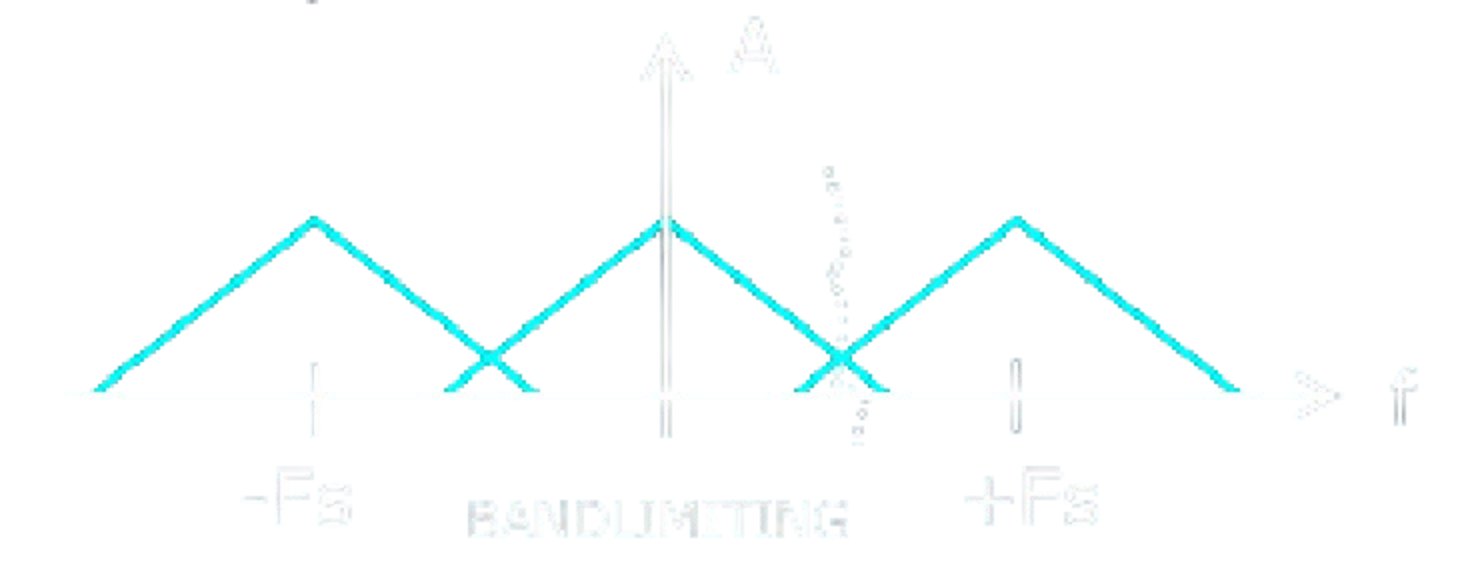
L’operazione di campionamento di un segnale periodico a tempo discreto genera un segnale con spettro periodico ripetuto ad intervalli Fs, con Fs Sampling frequency.
Bisogna quindi ritagliare la porzione di spettro fino a mediante l’uso di un filtro Filtro passa banda per rispettare il Teorema di Nyquist ed evitare che si crei Aliasing.
Lo spettro di un segnale campionato è dato dalla Convoluzione dello spettro del segnale con quello di un Treno di impulsi.
Risulta quindi un segnale scalato e ripetuto ogni frequenza .
Più generalmente è possibile trovare la DFT campionando il risultato in frequenza della DTFT lungo un solo periodo in N punti equidistanti (generalmente 1024 o 2048). La precisione della DFT cresce al crescere di N.
Link to original
La DFT è molto sensibile al fenomeno di Spectral Leakage.
DFT e DTFT
Notare che la DFT e la DTFT non sono la stessa cosa.
La DTFT è continua nel dominio della frequenza, il passaggio che collega le due è il campionamento dell’output della DTFT per generare la DFT e potervi lavorare con un computer che lavora a numeri finiti.
| Segnali a tempo continuo | Segnali a tempo-discreto | |
|---|---|---|
| Segnali periodici | Serie di Fourier | Discrete-time Fourier Transform |
| Segnali aperiodici | Continuous Fourier Transform | Discrete Fourier Transform |