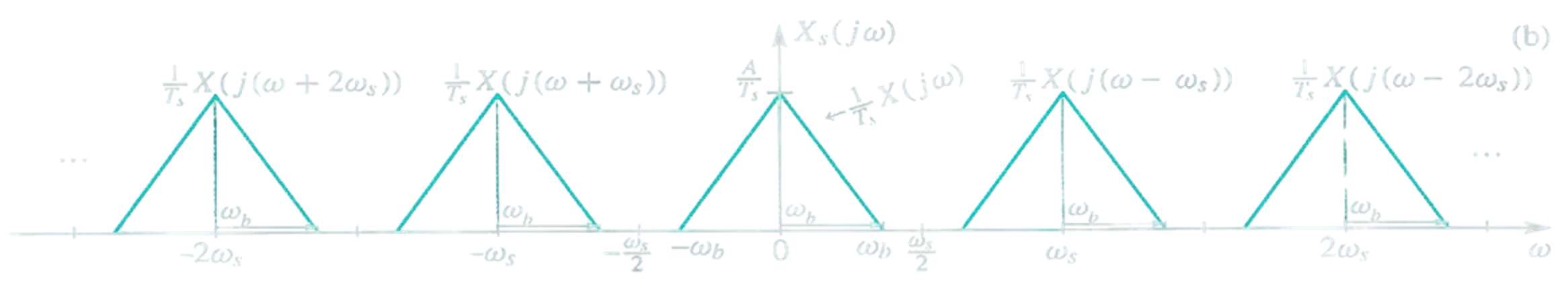Lezione 4

Low Level Quantization Noise

Quando un segnale viene quantizzato, gli intervalli tra i livelli discreti creano una sorta di “approssimazione” del segnale originale. La differenza tra il valore effettivo e il valore quantizzato introduce un errore, noto come errore di quantizzazione, che appare nel segnale sotto forma di rumore. Questo rumore è casuale e viene distribuito su tutta la gamma di frequenze del segnale.

Quando il livello di un segnale è molto basso, ad esempio nelle parti più silenziose di una registrazione audio, diventa particolarmente evidente l’effetto del rumore di quantizzazione. Ciò è dovuto a due fattori principali:

1. Numero limitato di livelli di quantizzazione disponibili a bassi volumi: Nei segnali deboli, l’ampiezza è vicina al livello zero. Poiché i livelli discreti di quantizzazione sono limitati, nelle sezioni a basso volume ci sono meno livelli disponibili per rappresentare accuratamente il segnale. Questo fa sì che l’errore di quantizzazione risulti relativamente più grande rispetto al segnale stesso.

2. Mancanza di mascheramento da parte del segnale principale: Quando l’ampiezza del segnale è alta, il rumore di quantizzazione è spesso mascherato dal segnale stesso e risulta quindi meno udibile. Tuttavia, a bassi livelli, il rumore diventa più udibile e può manifestarsi come un “fruscio” o “granulosità” udibile.

Un metodo comune per minimizzare l’effetto del low-level quantization noise è il Dithering.
Il dithering consiste nell’aggiungere un leggero rumore casuale al segnale prima della quantizzazione. Questo rumore maschera il rumore di quantizzazione e lo rende meno percepibile, distribuendo l’errore in maniera più uniforme e meno invasiva. Sebbene il dithering introduca esso stesso una sorta di rumore, questo tende a essere meno fastidioso rispetto al rumore di quantizzazione percepibile a bassi livelli.

---

I think a better term for quantization noise is simply “error.” When you digitize a signal voltage, there are a finite number of digital levels (numbers) you can use to describe it. The error is the difference between the actual, analog voltage level, and the digital level you use to represent it.

In signal processing terms, error is “information loss.” An analog signal has an infinite amount of information — any way you measure the voltage can be infinitely subdivided. A digital signal has a finite amount of information. When you digitize a signal, you lose information, and it can never be recovered.

What’s in that information? It’s unknown. If there are no biases in your system, it’s random. A random signal is noise.

So that’s where the terms come from.

Can you actually hear that noise? Mathematically, it’s definitely there; but does it sound like “white noise?” I’m a little unclear on that myself.

I find it easier to understand in visual terms. In image digitization, quantization error looks like color banding. If you have a continuous color gradient, artifacts due to color bit depth appear as “stripes” in the gradient. The lower the bit depth, the wider the bands.

The math, and, in fact, the tech is identical between the domains. It’s just our senses which are different. The audio equivalent of quantization error is what color banding “sounds” like.

ananbd on Reddit

Vedi anche: Quantizzazione, Dithering

Link to original

Dithering

Il Dithering, nella elaborazione numerica di segnali, è una forma di rumore con una opportuna distribuzione, che viene volontariamente aggiunto ai campioni con l’obiettivo di minimizzare la distorsione introdotta dal troncamento nel caso in cui si riquantizzino i campioni stessi. Il dithering viene usato abitualmente nell’elaborazione di segnali video e audio campionati e quantizzati. Il dithering non ha nulla a che vedere col jitter. È invece correlato con la risonanza stocastica in fisica, in cui la presenza di rumore stocastico aumenta la risposta di un segnale a perturbazioni esterne.

Wikipedia

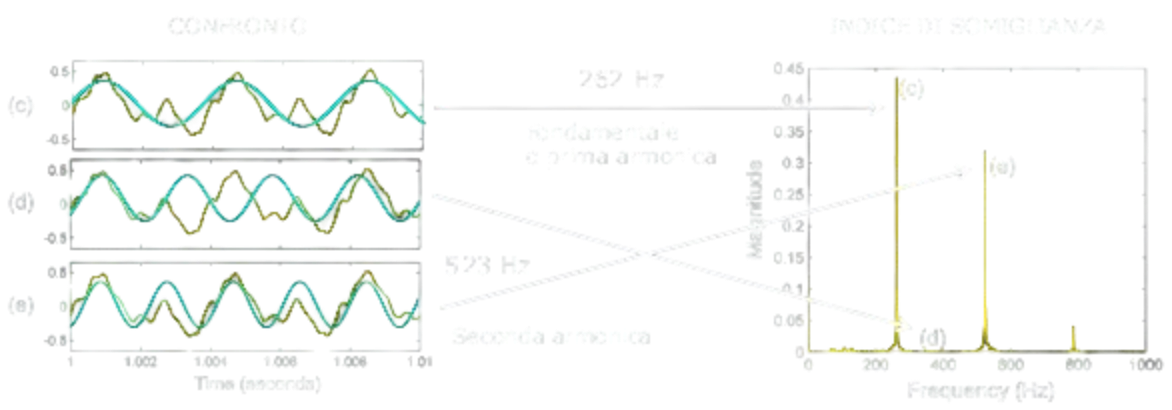
Il dithering ad esempio viene usato molto nel caso in cui vi siano segnali troppo piccoli e che vengono quantizzati con pochi LSB rispetto al fondo scala. Quando questo accade il segnale assume una forma simile ad un’onda quadra che nello spettro di potenza presenta diverse armoniche.

Il tempo ha provato empiricamente che per l’orecchio umano è preferibile ascoltare un segnale con un po’ di rumore scorrelato
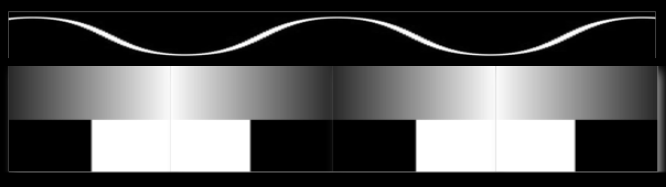
piuttosto che un segnale con tante armoniche, che sono correlate al segnale principale.

Prendendo per esempio questa immagine, si ha che 1 è nero, 0 è bianco. Qualunque segnale maggiore di 0.5 viene considerato nero, viceversa bianco. Se si aggiunge un rumore uniforme di intensità casuale tra 0 e 0.5, si ottiene un’immagine percettivamente simile a quella originale utilizzando soltanto due colori. Un concetto simile può essere applicato all’elaborazione audio.

Vedi anche: Low Level Quantization Noise

Link to original

Trasformata di Fourier

In analisi matematica, la Trasformata di Fourier è una trasformata integrale, cioè un operatore che trasforma una funzione in un’altra funzione mediante un’integrazione. Trova numerose applicazioni nella fisica e nell’ingegneria ed è uno degli strumenti matematici maggiormente utilizzati nell’ambito delle scienze pure e applicate, permettendo di scrivere una funzione dipendente dal tempo come combinazione lineare (eventualmente continua) di funzioni di base esponenziali.

La trasformata di Fourier associa a una funzione i valori dei coefficienti di questi sviluppi lineari, dandone in questo modo una rappresentazione nel dominio delle frequenze che viene spesso chiamata spettro della funzione (la relazione con il concetto di spettro di un operatore può essere compresa se si considera l’operatore di convoluzione con la funzione in esame). A volte si intende per trasformata di Fourier la funzione che risulta dall’applicazione di questo operatore.

Wikipedia

In termini semplici, la trasformata di Fourier permette di passare da una rappresentazione nel dominio del tempo (o spazio) a una rappresentazione nel dominio delle frequenze. Se abbiamo una funzione $f(t)$ che descrive un segnale nel tempo, la sua trasformata di Fourier $F(\omega )$ ci darà una descrizione di quel segnale in termini delle sue frequenze componenti.

Si può sintetizzare il suono analogico tramite la trasformata inversa, ovvero la sintesi di Fourier.

L’analisi di Fourier si può presentare in diverse modalità in base al tipo di segnale da analizzare.

Tipi di segnale

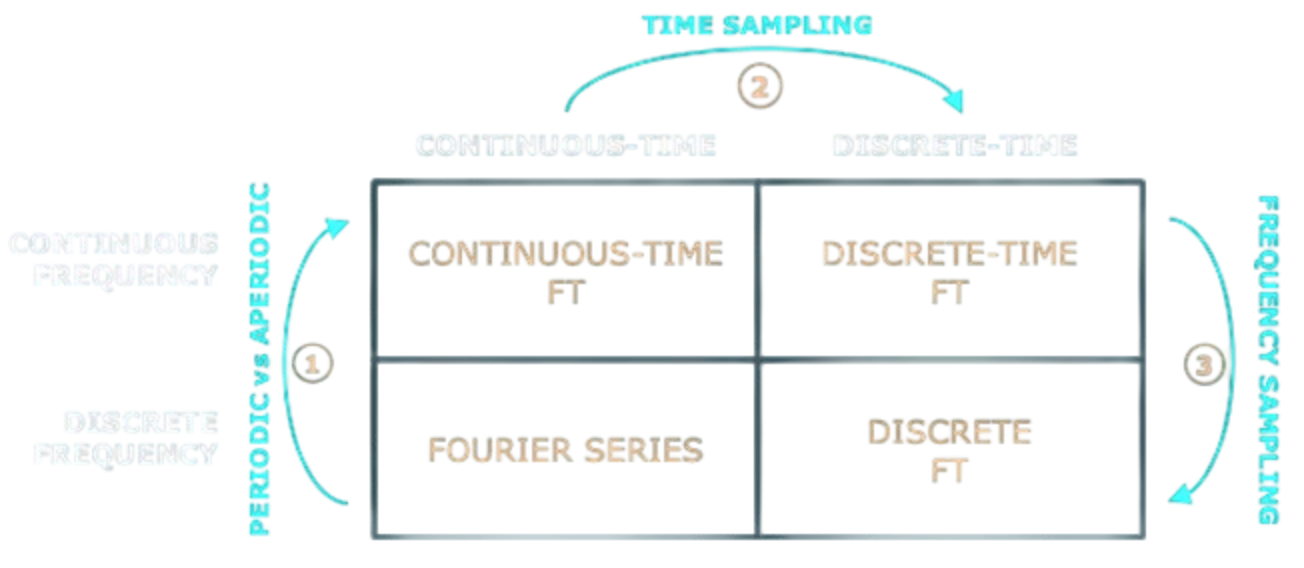
Un segnale può essere continuo o discreto nel tempo.
Quando un segnale è continuo nel tempo, la trasformata di Fourier sarà discreta in frequenza, e viceversa.
Quindi tramite le operazioni di Campionamento e Quantizzazione si ottiene una trasformata di Fourier continua nel tempo.

Serie di Fourier

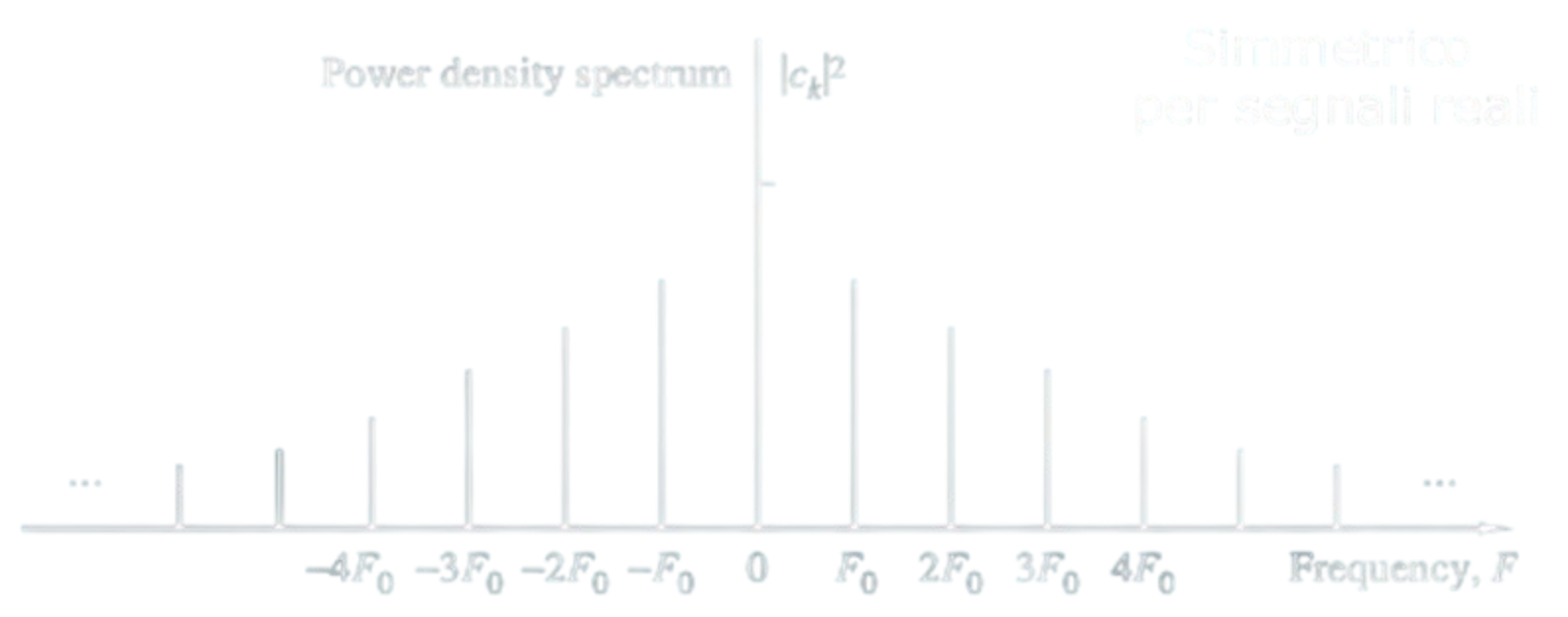
Nel caso di segnali periodici continui si realizza la conversione tempo / frequenza tramite la Serie di Fourier, che descrive un segnale una somma pesata di sinusoidi armoniche, multiple della frequenza principale di un multiplo k intero. Se il coefficiente k non fosse intero il segnale non potrebbe essere periodico.
Il segnale in frequenza è la densità spettrale di potenza, non energia, in quanto l’energia dei segnali periodici è infinita.

Link to original

Discrete Time Fourier Transform

In matematica, la trasformata di Fourier a tempo discreto (DTFT) è una forma di analisi di Fourier applicabile a una sequenza di valori discreti.
La DTFT viene spesso utilizzata per analizzare campioni di una funzione continua. Il termine tempo discreto si riferisce al fatto che la trasformata opera su segnali aperiodici a tempo discreto.
$F\{x_s(t)\}={\sum }_{n=-\infty }^{\infty }x(n{T}_s)e^{-j\omega (n{T}_s)}$
dove $n{T}_s$ indica multipli del periodo di campionamento $T_s$ e la frequenza dello spettro $\omega$ è continua.

Wikipedia

Link to original

Discrete Fourier Transform

L’operazione di campionamento di un segnale periodico a tempo discreto genera un segnale con spettro periodico ripetuto ad intervalli Fs, con Fs Sampling frequency.
Bisogna quindi ritagliare la porzione di spettro fino a $\frac{Fs}{2}$ mediante l’uso di un filtro Filtro passa banda per rispettare il Teorema di Nyquist ed evitare che si crei Aliasing.

Lo spettro di un segnale campionato è dato dalla Convoluzione dello spettro del segnale con quello di un Treno di impulsi.
$X_s({\omega }_s)=X(\omega )\ast {\sum }_{n=-\infty }^{+\infty }\frac{1}{T}\delta (\omega -n{\omega }_s)=\frac{1}{T_s}{\sum }_{n=-\infty }^{+\infty }X(\omega -n{\omega }_s)$
Risulta quindi un segnale scalato e ripetuto ogni frequenza $F_s={\omega }_s$.

Più generalmente è possibile trovare la DFT campionando il risultato in frequenza della DTFT lungo un solo periodo in N punti equidistanti (generalmente 1024 o 2048). La precisione della DFT cresce al crescere di N.
La DFT è molto sensibile al fenomeno di Spectral Leakage.

Link to original

DFT e DTFT

Notare che la DFT e la DTFT non sono la stessa cosa.
La DTFT è continua nel dominio della frequenza, il passaggio che collega le due è il campionamento dell’output della DTFT per generare la DFT e potervi lavorare con un computer che lavora a numeri finiti.

	Segnali a tempo continuo	Segnali a tempo-discreto
Segnali periodici	Serie di Fourier	Discrete-time Fourier Transform
Segnali aperiodici	Continuous Fourier Transform	Discrete Fourier Transform

Link to original

Timbro

Il timbro è quella particolare qualità del suono che permette di distinguere due suoni con uguale frequenza o altezza. Il timbro rappresenta quell’attributo della sensazione uditiva che consente all’ascoltatore di identificare la fonte sonora, rendendola distinguibile. Il timbro, dunque, è la qualità di un suono.

Si può dire, con linguaggio non tecnico, che il timbro è il particolare profilo o carattere distintivo di un suono emesso da una voce o strumento musicale: una chitarra elettrica e un oboe emettono la medesima nota (stessa altezza, ossia frequenza) con timbri inconfondibilmente diversi e peculiari, e così avviene per le voci umane o i versi animali.

Wikipedia

Il timbro è uno delle tre Caratteristiche soggettive del suono insieme a intensità soggettiva o loudness e Altezza tonale.

Link to original