Esempi di domande

WARNING

Alcune risposte potrebbero essere state raffinate parzialmente tramite ausilio di intelligenza artificiale, ma sono sempre state scritte in partenza a mano (give me a break, faccio schifo a scrivere in italiano)

Descrivere la Relazione Che Lega Frequenza F E Lunghezza d’onda Λ Di un’onda Acustica Armonica. Discutere, Con Un Esempio a Scelta, Le Implicazioni Pratiche Che Derivano Dalla Variabilità Di Λ Nel Campo Delle Frequenze Udibili. (2 punti)

La relazione che lega la frequenza $f$ e la lunghezza d’onda $\lambda$ prevede anche il conoscere la velocità di trasmissione $v$ dell’onda.
$\lambda =\frac{v}{f}$
Quindi a parità di velocità, onde ad alta frequenza hanno una lunghezza minore, mentre onde a bassa frequenza hanno una lunghezza maggiore.

L’udito umano riesce a silentire dai 16Hz a circa 20kHz, dove generalmente si parla di bassa frequenza fino a 300Hz, media fino a 2000Hz ed alta frequenza dopo i 2000Hz.
Inoltre la sensibilità dell’udito non è uniforme attraverso tutte le frequenze, ma l’orecchio è più sensibile tra i 2kHz e 5kHz, dove le curve isofoniche risultano perlopiù piatte.

Questo implica che quando si fa equalizzazione di una traccia sonora complessa spesso si da un boost a determinate frequenze per renderle più apprezzabili dall’orecchio, mentre ad esempio i sibilii a cui l’orecchio è molto sensibile si attenuano.

Vedi anche:Curve Isofoniche

Descrivere Le Curve Isofoniche dell’audiogramma Normale, Inclusa la Soglia Di Udibilità, E Spiegare la Differenza Fra Livello Di Pressione Sonora in dB E Livello Di Sensazione Sonora in Phon. (3 punti)

L’udito umano è sensibile alle frequenze tra 16 Hz e 20 kHz circa, ma la sensibilità non è uniforme. L’orecchio percepisce meglio le frequenze tra 2 e 5 kHz, range cruciale ad esempio per la comprensione del parlato. Curve isofoniche, ottenute con studi sperimentali, descrivono la sensibilità a diverse frequenze. Sono graficate con frequenza (Hz) in ascissa e livello di pressione sonora (dB SPL) in ordinata. Il phon esprime l’intensità sonora percepita, definita come il livello di pressione sonora di un suono puro a 1 kHz.

Curve come quella a 40 phon includono suoni percepiti intensi come un suono puro a 1 kHz e 40 dB SPL.

Un audiogramma normale umano è decrescente fino ai 1000Hz, e poi crescente dopo i 5kHz, con un picco locale attorno tra i 2kHz e 5kHz. Ritorna decrescente dopo i 10kHz. Quindi mostra una maggiore sensibilità (minimi SPL) tra 2 e 5 kHz, con ridotta sensibilità alle basse (10 kHz) frequenze.

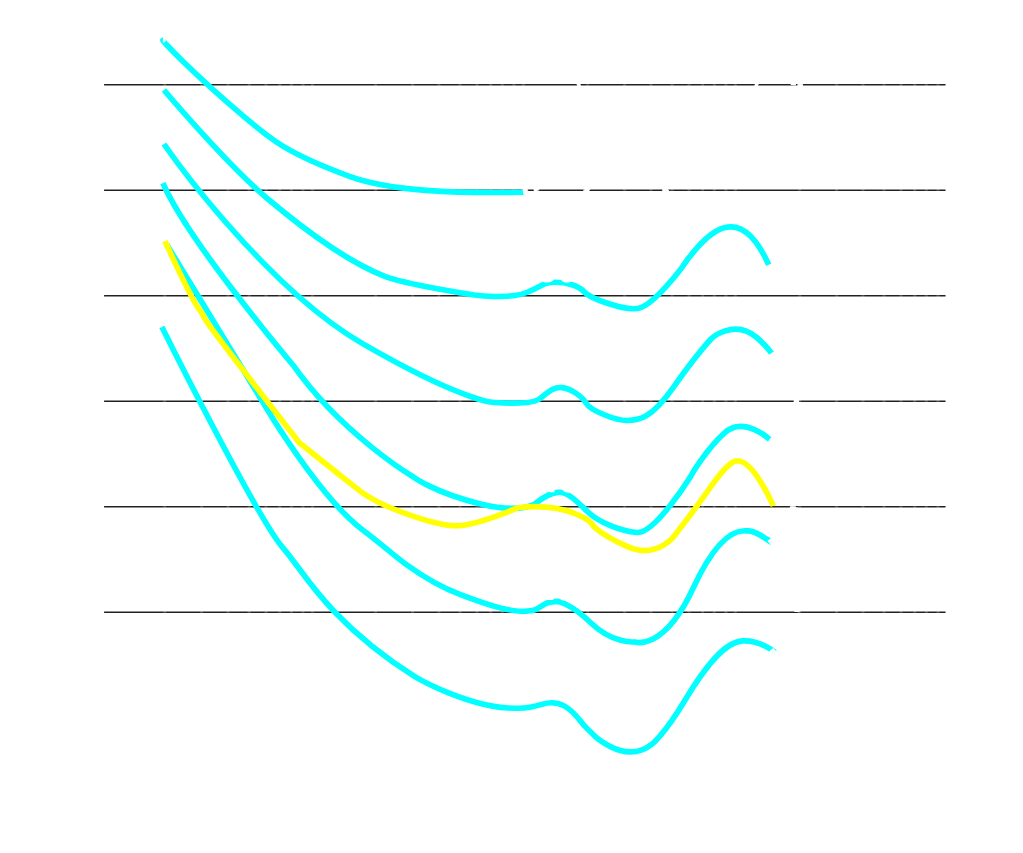
Il livello di pressione sonora indica la pressione fisica delle onde sonore rispetto a $20\mu Pa$, mentre il Phon si basa sulla percezione soggettiva che l’uomo ha del suono. Questi coincidono soltanto alla frequenza pura di 1kHz, che è proprio la definizione di Phon.

Vedi anche: Phon, SPL

Riportare Indicativamente I Valori Della Frequenza Centrale Di Un Filtro a Bande d’ottava. (1 punto)

I filtri a bande d’ottava sono dei filtri che dividono lo spettro esattamente in ottave, ovvero la distanza tra la frequenza massima del filtro e la minima è un’ottava. Utilizzano come frequenze centrali le frequenze dei Do, ovvero (in maniera approssimata) 16Hz, 32Hz, 64Hz, e così via secondo la legge: $f(i)=16\cdot 2^{(i-1)}$ , partendo con indice 1.

(Bonus) In realtà secondo l’ISO 266 vi è una leggera differenza in quanto le frequenze sarebbero 16Hz, 31.5Hz, 63Hz, 125Hz, 250Hz, etc…, ma la formula è un’approssimazione delle frequenze dell’ISO, soprattutto a frequenze medio-basse.

Vedi anche: Scala d’ottava

Riportare Indicativamente Gli Intervalli Di Frequenza Corrispondenti Alle Basse, Medio-basse, Medio-alte E Alte Frequenze. (1 punto)

Si parla di frequenze basse fino ai 300Hz, medio-basse 300Hz e 1000Hz, medio-alte tra i 1000Hz e 2000Hz ed alte dopo i 2000Hz.
La maggior parte del parlato umano va nelle frequenze medie.

Descrivere I Meccanismi Che Regolano la Nostra Percezione Della Posizione Di Una Sorgente Sonora. Su Quali Informazioni Si Basano, Su Che Frequenze Lavorano? (3 punti)

Le nostre orecchie utilizzano due fattori per stabilire la posizione dei suoni: differenza di intensità del suono tra orecchio destro e orecchio sinistro e latenza del suono tra orecchio destro e orecchio sinistro. Questi vengono detti Interaural Time Difference e Interaural Intensity Difference.

Il primo si basa sul fatto che un suono, a meno che non sia perfettamente parallelo all’asse mediano dell’ascoltatore (frontale o posteriore) impiega un tempo diverso per arrivare alle orecchie.

Il secondo invece analizza l’intensità delle frequenze del suono, in quanto quando il suono sbatte sulla testa, le alte frequenze vengono riflesse, le basse frequenze invece vengono rifratte, modificando l’intensità del suono a specifiche frequenze. L’IID quindi è prevalente a frequenze, mentre l’ITD è prevalente ad alte frequenze.

Vedi anche: Interaural Time Difference, Interaural Intensity Difference

Definire Che Cosa Si Intende per “dB Full scale” (dBFS), come Viene Misurato, E Cosa Si Intende per Dynamic Range. Precisare Inoltre come Si Differenzia Il dBFS Dalla Misura Dei dB SPL. (2 punti)

Il dBFS è una scala di misura dell’intensità di un suono relativo alla massima intensità possibile senza ottenere distorsioni, detta appunto Full Scale.
Questo perché ogni quantizzatore utilizza un numero finito di bit (generalmente 16, 24, per i più costosi 32) per quantizzare delle intensità sonore. Se l’intensità sonora è maggiore rispetto a quella di fondo scala si ottiene distorsione del segnale.

Quindi quando si usano i dBFS si assegna a 0dB il valore massimo possibile dal volume di una traccia, e il resto dei valori sono negativi, e relativi al valore di fondo scala assegnato.

Il dBFS di un suono si calcola quindi come $20\cdot \log \frac{A}{A_{max}}$.

Il range di un segnale è la distanza tra un il volume massimo e minimo rappresentabile da un segnale. Questo dipende dalla risoluzione in bit, in quanto per ogni bit l’SNR migliora di circa 6dB, per cui a 16bit ad esempio equivale a $6\cdot 16=96dB$.

Infine, i dB SPL rappresentano l’intensità fisica dell’onda sonora che viene trasmessa e sono misurati con riferimento a $20\mu Pa$. Invece i dBFS sono una misura inerente puramente al dominio digitale, non fisico.

Vedi anche: dBFS, Dynamic Range, SPL

Rappresentare E Commentare Il Diagramma Della Variazione dell’SNR in Funzione Del Rapporto Tra Dinamica Del Segnale (σ) E Intervallo Di Quantizzazione (xol) per Un Quantizzatore Uniforme Su N Bit (anche Al Variare Del Numero Di bit). (3 punti)

Orcodue poi lo faccio

Descrivere Le Ragioni Alla Base Di Un Quantizzatore Non-uniforme, Le Sue Caratteristiche E I vantaggi/svantaggi Che Ne Derivano Rispetto Ad Un Quantizzatore Uniforme. E’ Possibile Parlare Di SNR Che Non Dipende Dal Livello Del Segnale, Perché?

Un quantizzatore uniforme divide il suo fondo scala in valori tutti uguali, creando una sorta di scala in cui ogni gradino ha altezza fissa. Viceversa un quantizzatore non-uniforme non rispetta questa proprietà.

Tuttavia spesso i segnali ad altezza minore rappresentano silenzio e/o rumore, che quindi non aggiunge informazione al segnale, togliendone però alle parti che effettivamente rappresentano del parlato. Questo riduce notevolmente l’SNR del segnale. Quindi il motivo principale è quello di ottimizzare la quantizzazione attorno alla gamma dinamica del segnale che si vuole rappresentare (rappresentare musica è molto diverso dal rappresentare del parlato).

Vedi anche: Quantizzazione, Errore di quantizzazione, SNR

Descrivere L’algoritmo Di Dithering per la Riduzione Della Distorsione Armonica. In Quali Casi È Consigliato? Come Modifica l’SNR Del Segnale? (4 punti)

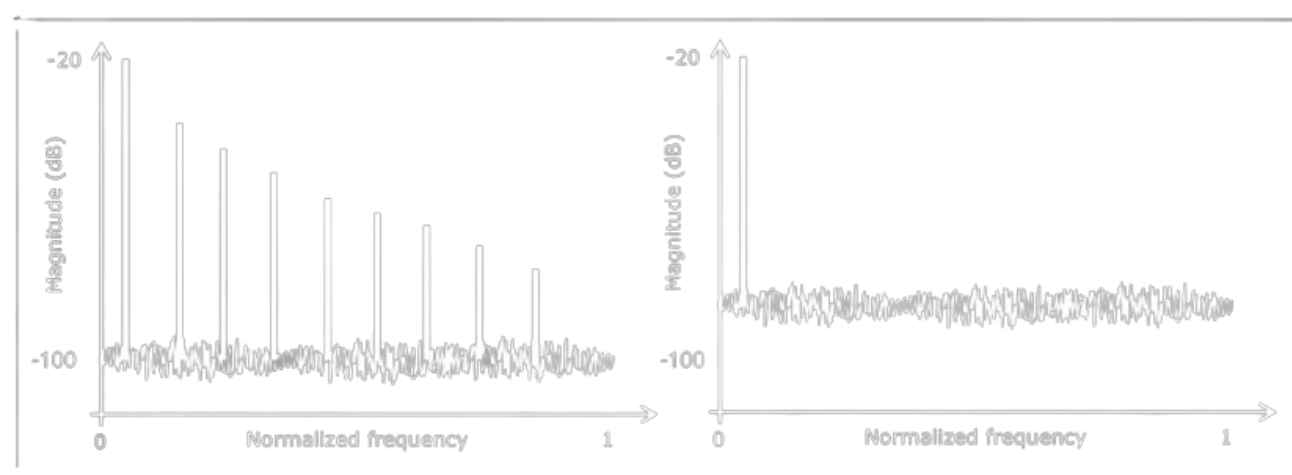
Il dithering permette di migliorare la qualità percepita del segnale in casi in cui il segnale è di partenza di bassa qualità. In particolare viene utilizzato in casi in cui si ha alta distorsione armonica o in caso di del low-level quantization noise, ovvero quando il segnale utilizza pochi livelli di quantizzazione rispetto a quanti supportati dal fondo scala.

Il dithering aggiunge del rumore casuale uniformemente distribuito, riducendo quindi la qualità del segnale in termini di SNR, tuttavia il rumore aggiunto è di bassa ampiezza (massimo 3dB) ed è percettivamente più gradevole rispetto ad una distorsione armonica.

Sebbene l’SNR peggiori, la perdità è bassa ed è accettabile in confronto al miglioramento percettivo del segnale. Inoltre aggiungendo rumore in maniera uniforme migliora anche l’uniformità dell’SNR, uniformando anche la qualità del segnale.

Vedi anche: Distorsione armonica, Low Level Quantization Noise, SNR, Dithering

Dato Un Frame Audio Di L=1024 Campioni a 48 kHz Su Cui Viene Applicata Una DFT Con N=2048, a Quale Intervallo Di Frequenze Corrisponde Il Bin Numero 128? (1 punto)

Nella DFT N rappresenta il numero di bin discreti.
Il k-esimo bin è centrato in $f_k=k\cdot \Delta f$ ed è largo $\Delta f$.

Si può trovare $\Delta f$ come il rapporto tra la frequenza di campionamento e il numero di bin, $\Delta f=\frac{f_k}{N}$.

Quindi in questo caso, $\Delta f=23.437Hz$, e considerando che si parte da zero il centro è $f_{128}=128\cdot 23.437=3000Hz$.
Ogni bin è largo proprio 23.437Hz quindi basta sottrarre (o aggiungere) la metà per trovare gli estremi.

Quindi il bin 128 corrisponde all’intervallo [2987.8Hz e 3011.7Hz].

Descrivere l’effetto Della Finestratura Nel Calcolo Della Trasformata Di Fourier Di Breve Termine (STFT). Quali Sono Le Caratteristiche Degli “artefatti” Introdotti? Da Cosa Dipendono? Fornire Un Esempio Grafico.

Warning

Risposta verificata MA generata da IA

La finestratura influisce direttamente sulla qualità della rappresentazione spettrale del segnale. Due principali artefatti sono:

Allargamento spettrale (Smearing)

• Effetto: Le frequenze strette o pure (come i toni sinusoidali) si estendono su un intervallo più ampio nello spettro anziché concentrarsi in un singolo bin di frequenza.
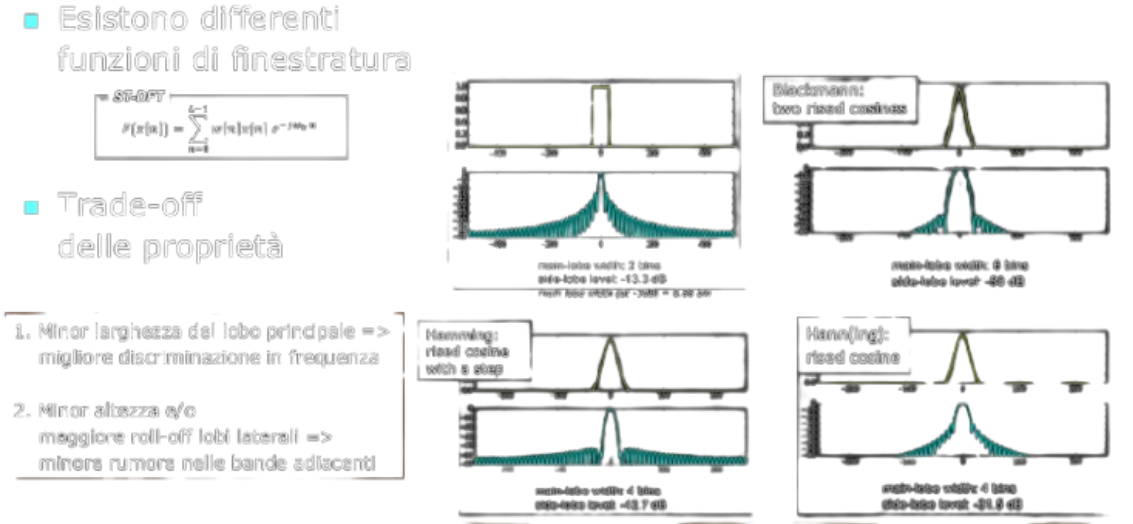
• Dipendenza: L’allargamento spettrale è correlato alla larghezza del principale “lobo” della funzione finestra nel dominio della frequenza. Finestrature con larghi lobi principali allargano lo spettro di una componente pura a più bin.
• Soluzione: Per minimizzare il problema si usano finestre con lobi principali stretti, come la Hann o la Hamming.

Leakage spettrale (alias “effetto di dispersione”)

• Effetto: Potenza di frequenze lontane dalla frequenza nominale di un segnale si “diffonde” nei bin vicini e in altri bin dello spettro.
• Dipendenza: È legato alla presenza di lobule laterali nella funzione finestra. Minori sono i lobule della finestra, minore sarà il leakage.
• Soluzione: Si preferiscono finestre con lobule laterali di ampiezza ridotta, come la finestra Hann o Kaiser.

Da cosa dipendono gli artefatti?
Gli artefatti di allargamento e leakage dipendono da:

1. Tipo di finestra scelta:
   • Finestra Rettangolare: Introduce leakage elevato e artefatti significativi.
   • Finestra Hann e Hamming: Riducono il leakage ma aumentano l’allargamento spettrale.
   • Finestra Blackman-Harris: Miglior compromesso tra leakage e allargamento.
2. Lunghezza della finestra (( L )):
   • Finestre più lunghe (( L ) grande) migliorano la risoluzione in frequenza ma peggiorano la risoluzione temporale.
   • Finestre più corte (( L ) piccolo) migliorano la risoluzione temporale, ma peggiorano quella in frequenza.

Vedi anche: Framing

Descrivere I Concetti Alla Base Dei Quattro Tipi Di serie/trasformate Di Fourier, a Quali Tipologie Di Segnali Si Applicano E la Derivazione Della Trasformata Discreta a Partire Dalla Serie / Trasformata Continua Di Fourier.

L’analisi di Fourier è un’operazione fondamentale per l’analisi dei segnali. Questa permette di visualizzare la distribuzione di un segnale nello spettro delle frequenze, ed ha diverse modalità d’uso in base alla classificazione del segnale tra tempo continuo o tempo discreto e periodico o aperiodico.

La periodicità in particolare è una caratteristica che difficilmente si trova in natura, in quanto per definizione un segnale periodico non ha mai fine.

1. Per i segnali a tempo continuo periodici, si usa una semplice Serie di Fourier, che descrive uno spettro discreto di tipo armonico in cui vi sono tutte le frequenze a multipli interi della frequenza fondamentale.
2. Per i segnali a tempo discreto periodici si usa una versione della Trasformata di Fourier che invece di utilizzare una formula integrale per il calcolo usa una sommatoria infinita detta Discrete Time Fourier Transform.
3. Per i segnali a tempo continuo aperiodici

Vedi anche: Analisi di Fourier

Spiegare I vantaggi/svantaggi nell’utilizzo Di Finestre Di Analisi corte/lunghe per l’analisi tempo/frequenza Di Un Segnale Audio Non Stazionario E come Possono Essere in Parte Mitigati (eventualmente Anche Con l’uso Di Finestre diverse).

Esprimere la Formula per Il Calcolo Dello Zero Crossing Rate. Per Quale Tipo Di Classificazione Audio È Utile? Perché? (2 punti)

Lo Zero Crossings Rate rappresenta il numero di volte in cui il segnale attraversa lo zero. Questo, applicato su adeguate finestre di analisi, permette di riconoscere segmenti di segnali ad alta frequenza o bassa frequenza (maggiore è la frequenza, maggiore sarà il tasso di attraversamenti dello zero).

Si può ad esempio utilizzare per distinguere il parlato da strumenti ad alta frequenza come gli strumenti a percussione. Inoltre si può utilizzare come de-esser, ovvero filtro che riduce le sibilanti nella voce.

Dato un frame x lungo L campioni, si può trovare come:
$\frac{{\Sigma }_{n=1}^L|sign[x_n]-sign[x_{n-1}|}{2L}$

def zcr(x):
	return len(np.nonzero(np.diff(np.sign(x)))[0])/len(x)

NOTE

Nota bene: l’accesso tramite indice viene utilizzato per np.nonzero, in quanto questo ritorna una tupla e bisogna prendere il primo valore della tupla.

Vedi anche: Zero Crossings Rate

Esprimere la Formula per Il Calcolo Del Centroide Spettrale E Della Varianza Spettrale. Descrivere Cosa Caratterizzano in Un Segnale Audio E, per Una Delle due Misure, Fornire due Esempi Di Spettri in Cui Il Calcolo Della Misura Risulti Significativamente Diverso. (2 punti)

Il centroide spettrale è una misura usata nell’elaborazione audio per rappresentare la distribuzione dello spettro di un suono, in particolare del suo centro di massa. La varianza spettrale, invece, ne descrive la varianza rispetto al centro di massa. Sostanzialmente si rifanno a centro di massa e varianza statistici, ma applicati all’elaborazione dell’audio digitale.

$C_i=\frac{{\sum }_{k=1}^{W_{fl}}k{X}_i(k)}{{\sum }_{k=1}^{W_{fl}}{X}_i(k)}$
$S_i=\sqrt{\frac{{\sum }_{k=1}^{W_{fl}}(k-C_i{)}^2{X}_i(k)}{{\sum }_{k=1}^{W_{fl}}{X}_i(k)}}$
Il concetto di Varianza Spettrale spesso viene accomunato alla banda del segnale, in quanto questi sono proporzionali. Ad esempio in segnali di tipo rumore, sia banda che varianza spettrale sono molto ampi, mentre in segnali a banda più ristretta e toni semplici anche la Varianza Spettrale è ridotta.

Vedi anche: Centroide Spettrale, Varianza Spettrale

Rappresentare Tramite Diagramma la Funzione Di Trasferimento Di Un Compressore [espansore] Audio, Descriverne Il Comportamento E Indicare Quali Sono I Parametri Che Ne Controllano Il Funzionamento. (2 punti)

Il compressore è un processore di dinamica che data una soglia S in (dB), riduce l’intensità del suono al di sopra della soglia di un ratio R e aumenta tutti quelli al di sotto della soglia.

Compressione sottrattiva	Compressione additiva

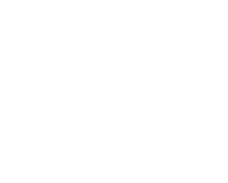I parametri dei compressori sono:

• Soglia S in dB
• Ratio R, comunemente 2:1, 4:1
• Knee, che indica lo smussamento dell’angolo di attacco
• Tempo di attacco, il tempo che impiega per attenuare del ratio stabilito
• Tempo di rilascio, il tempo che impiega per tornare al ratio 1:1

Il caso limite di un compressore con ratio molto alta è quello del limitatore, che taglia tutti i segnali che superano una certa intensità in dB.

L’opposto del compressore è l’espansore, che aumenta tutti i suoni che hanno un’intensità minore di una determinata soglia S e diminuisce tutti quelli al di sopra della soglia. I parametri sono gli stessi, ma il caso limite per una ratio molto alta è il noise gate.

Vedi anche: Compressore, Espansore, Limitatore, Noise Gate

Spiegare Il Funzionamento dell’audio Stereofonico per Il Posizionamento Del Segnale Audio: Su Quale Principio Si Basa per Creare l’illusione Uditiva, in Che Condizioni È Efficace, Quali Sono I Limiti. Tracciare Una Rappresentazione Schematica Del Sistema.

L’audio stereofonico utilizza il fatto che gli umani hanno due orecchie per creare una rappresentazione tridimensionale del suono sfruttando due proprietà: intensità sonora e ritardo del suono. Questi vengono detti Interaural Time Difference ed Interaural Intensity Difference.

Si usano due altoparlanti piazzati ai vertici di triangolo equilatero che riproducono suono sincronamente per creare una sorgente sonora fantasma che permette di posizionare il suono lungo la circonferenza che li unisce, a patto che l’ascoltatore si trovi al rimanente vertice del triangolo, posizione detta sweet spot. Questo è effettivamente il limite del sistema, ovvero perché la stereofonia sia ottimale l’utente deve trovarsi ad una posizione precisa rispetto agli altoparlanti.

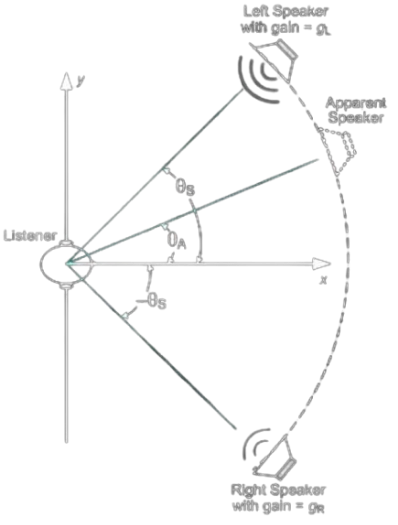
Vedi anche: Stereofonia, Interaural Time Difference, Interaural Intensity Difference

Descrivere Le Caratteristiche Dei Filtri Shelving (low E high) [oppure peak/notch] per l’equalizzazione Visti a Lezione. Fornire la Rappresentazione Grafica Nel Dominio Della Frequenza, l’indicazione Dei Parametri Con Cui È Possibile Controllarlo E Il Loro Effetto. (2 punti)

Un filtro di shelving, il cui nome deriva dall’inglese shelv, mensola, è un filtro che viene usato per aumentare o ridurre l’intensità di una specifica banda di frequenze senza andare a toccare l’intensità delle frequenze al di fuori della banda.
Infatti la differenza con il passa-basso (o alto) è che quest’ultimo annulla tutte le frequenze al di fuori della banda stabilita, mentre shelving no.

I parametri sono:

• Frequenza di taglio, al di sopra (high) o al di sotto (low) del quale applicare la correzione
• Pendenza della zona di transizione
• Guadagno (o attenuazione)

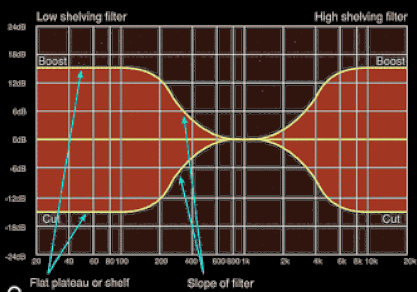
Vedi anche: Shelving Filter, Peak Filter

Disegnare due Esempi Di Spettri Di Un Segnale Audio, Uno Armonico E Uno Non Armonico. Per Lo Spettro Armonico, Indicare Da Cosa Sono Rappresentati Il Pitch, L’inviluppo E Le Formanti. (2 punti)

Uno spettro armonico è uno spettro la cui distribuzione principale è formata da una componente in frequenza principale (prima armonica o armonica fondamentale) $f_0$ e da tutti i suoi multipli interi.
Generalmente è legata a strumenti musicali, voce umana o segnali periodici puri.

Viceversa un segnale non armonico non segue questa proprietà.

Il pitch del segnale è la frequenza $f_0$ e rappresenta l‘“altezza” del suono. Ad esempio una voce femminile generalmente ha un pitch più alto di quella maschile.
Le formanti sono dei picchi (non multipli interi della frequenza fondamentale) che sono il risultato del filtraggio tramite sintesi sottrattiva del segnale armonico generato dalle corde vocali umano o dallo strumento musicale, filtro applicato nella cassa di risonanza (anche qui umana o musicale). Queste identificano il fonema o lo strumento musicale che che sta producendo il suono.
Ad esempio, due strumenti musicali che riproducono entrambi un Do a 64Hz avranno delle formanti diverse.
L’inviluppo è l’andamento nel tempo del segnale.

Vedi anche: Armoniche, pitch, Formante, Inviluppo

Fornire la Definizione Di Cepstrum, Spiegarne Il Significato E come Possono Essere Utilizzate Le Informazioni Da Esso Rappresentate, Eventualmente Con Alcune Trasformazioni. (3punti)

Il cepstrum è uno degli indicatori (e tipi di analisi) che vengono utilizzati per analizzare un segnale audio. Matematicamente è il risultato della trasformata di Fourier del logaritmo della trasformata di Fourier di un segnale.
$C=f[log(f[x])]$

Nel campo dell’analisi di un segnale realizzato tramite sintesi sottrattiva, l’analisi cepstrale riesce a separare nella prima ventina di coefficienti le informazioni sulla parte vocale del segnale da cui è possibile estrarre le feature delle formanti, e tramite un picco successivo a questi coefficienti è possibile trovare il pitch del segnale originale.

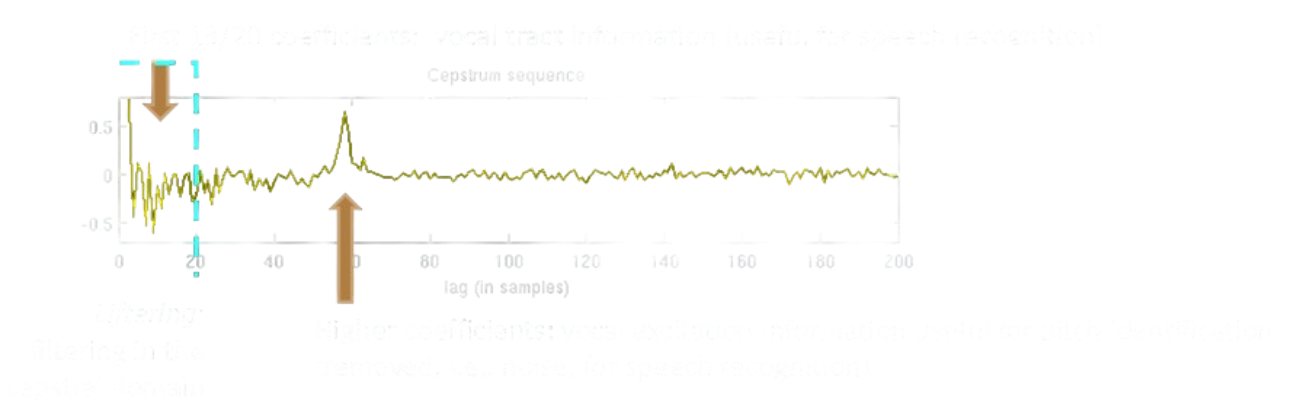
Si usa anche per trovare i Mel-Frequency Cepstrum Coefficients, che rappresenta informazioni simili all’analisi cepstrale ma in scala di percezione mel.

Vedi anche: Cepstral Analysis, MFCC, Scala mel

Descrivere Il Funzionamento Della Modulazione in Frequenza (FM) per la Sintesi Del Suono. Spiegare come Il Fattore C:M E l’indice Di Modulazione (I) Intervengono Nel Caratterizzare Lo Spettro Risultante E Perché. (4 punti)

Indicare Da Cosa Dipende l’SNR Della Sintesi Wavetable E, Indicativamente, in Quali Termini Di Grandezza.

Warning

Risposta del professore

L’SNR della sintesi wavetable dipende dalla grandezza (numero di campioni) della wavetable e dalla tecnica di
interpolazione. Indicativamente, ad ogni raddoppio del numero di campioni N consegue un incremento di “tot” dB che
è praticamente il doppio nel caso dell’interpolazione rispetto a troncamento e arrotondamento (che differiscono solo
di un offset). (+12, vs +6)

Scrivere Il Codice Python per Calcolare I Punti Di Una Sinusoide a Frequenza F Su Un Intervallo Di Un Secondo Assumendo Una Frequenza Di Campionamento Fs. (2 punti)

import numpy as np
import librosa
import matplotlib.pyplot as plt
 
F = 100
Fs = 500
duration = 1
 
x = np.arange(Fs*duration)/Fs
y = np.sin(2*np.pi*F*x)
 
plt.plot(x, y, color="red")
plt.xlim(left=0,right=duration)
plt.show()

Scrivere E Commentare Brevemente Il Codice Python per Massimizzare l’ampiezza Dei Valori (normalizzare) Un Segnale Audio Y Senza Causare Clipping. (1 punto)

import numpy as np
import librosa
import matplotlib.pyplot as plt
 
# Carica Suono "trumpet" Di Esempio
y, sr = librosa.load(librosa.ex('trumpet'), sr=None)
 
plt.plot(np.arange(len(y)), y)
plt.show()
 
def normalize(y):
# Prendi Il Massimo in Valore Assoluto per Cui Normalizzare
    max = np.max(np.abs(y))
    y = y/max
    return y
 
 
plt.plot(np.arange(len(y)), normalize(y))
plt.show()

Scrivere E Commentare Brevemente Il Codice Python per Caricare Il Segnale Audio Da Un File Denominato “prova.wav” E Visualizzarne in Un Grafico la Forma d’onda (ampiezza Vs tempo) Della Porzione Compresa Tra T0 = 57 S E T1 = 75.3 S

import numpy as np
import matplotlib.pyplot as plt
import librosa
 
start = 57
end = 75.3
 
y, sr = librosa.load("prova.wav", sr=None)
 
 
plt.plot(np.arange(len(y)), y)
plt.xlim(start*sr, end*sr)
plt.show()

Scrivere E Commentare Brevemente Il Codice Python Di Una Funzione Che Calcoli l’SNR Dati come Argomenti Il Segnale Originale E Quello Quantizzato. (1 punto)

import numpy as np
import matplotlib.pyplot as plt
import librosa
 
F = 100
Fs = 500
duration = 1
 
x = np.arange(Fs*duration)/Fs
y = np.sin(2*np.pi*F*x)
 
def quantize_uniform(x, qmin=-1.0, qmax=1.0, qlevel=8):
  qstep = (qmax-qmin) / qlevel
  xnorm = (x-qmin) * qlevel / (qmax-qmin)
  xnorm[xnorm > qlevel] = qlevel
  xnorm[xnorm < 0] = 0
  xnorm_quant = np.floor(xnorm)
  xquant = xnorm_quant * (qmax-qmin) / qlevel
  xquant = xquant + qmin + qstep/2
  return xquant
 
def SNR(original, quantized):
    noise = original - quantized
    return 10*np.log10(np.sum(original**2)/np.sum(noise**2))
 
print(SNR(y, quantize_uniform(y)))

Scrive E Commentare Brevemente Il Codice Python per Calcolare l’RMS in dBFS Su Frame Audio Successivi Parzialmente Sovrapposti Data Una Clip Audio Mono Memorizzata in Un Vettore Y E Una Frequenza Di Campionamento Sr.

import numpy as np
import librosa
import matplotlib.pyplot as plt
 
y, sr = librosa.load(librosa.ex("trumpet"), sr=None, mono=True)
 
def RMS(y, sr):
# Imposto Ogni Frame Di 0.02 Secondi
    frame_duration = 0.02 
# Calcola Durata Di Un Frame
    frame_length = frame_duration * sr
# Se la Lunghezza Del Frame È Dispari, la Rendo Pari Aggiungendo Un Sample Al Frame per Semplificarmi la Vita Dopo
    if(frame_length % 2 != 0):
        frame_length = frame_length + 1
 
# Padding
    #y = np.append(y, np.zeros(int(frame_length/2)))
 
# Trovo Il Massimo Volume
    RMS_FS = max(abs(y))
 
# Inizializzo Buffer
    rmsdbfs = np.array([])
    for i in range(0, len(y), int(frame_length/2)):
# Per Ogni Frame Calcola RMS in DBFS E Aggiungi Al Buffer
        frame = y[i:i+int(frame_length)]
        rms = np.sqrt(np.mean(frame**2))
        current_frame_dbfs = 20*np.log10(rms/RMS_FS)
        rmsdbfs = np.append(rmsdbfs, current_frame_dbfs)
    return rmsdbfs
 
rms_values = RMS(y, sr)
x_values = np.arange(0, len(rms_values), 1)
print(rms_values)
plt.plot(rms_values)
plt.show()
 
plt.plot(y)
plt.show()

Vedi anche: Framing, Root Mean Square, dBFS

Scrivere E Commentare Brevemente Il Codice Python Di Una Funzione Che Calcoli la DFT. La Funzione Riceva come Argomenti Un Frame Audio (x), Il Numero Di Valori Su Cui Calcolare la DFT (N) Ed Un Altro Parametro (che Lo Studente Deve identificare), E Ritorni Gli N Valori Della DFT E I Valori Delle Frequenze Corrispondenti Su Cui Sono Calcolati. (1 punto)

import numpy as np
import librosa
import matplotlib.pyplot as plt
 
y, sr= librosa.load(librosa.ex("trumpet"), sr=None)
 
def DFT(x, N, sr):
    val = np.fft.rfft(x, N)
    freq = np.fft.rfftfreq(N, d=1/sr)
    return val, freq
 
N = 1024
dft_values, freq_values = DFT(y[0:N-1], N, sr)
plt.plot(freq_values, np.abs(dft_values))
plt.show()

Vedi anche: DFT

Scrivere E Commentare Brevemente Il Codice Python per Calcolare Lo Spettrogramma Tramite Il Computo Della DFT Su Frame Audio Successivi Parzialmente Sovrapposti. Quale È la Sequenza Di Operazioni Necessarie E Quali I Parametri Da Utilizzare? (2 punti)

import numpy as np
import librosa
import matplotlib.pyplot as plt
 
y, sr = librosa.load(librosa.ex("trumpet"), sr=None, mono=True)
 
def DFT(x, N, sr):
    val = np.fft.rfft(x, N)
    freq = np.fft.rfftfreq(N, d=1/sr)
    return val, freq
 
def Spectrogram(y, sr):
    frame_duration = 0.02
    frame_length = int(frame_duration * sr)
    hop_length = int(frame_length/2)
 
    frames_number = int((len(y)-frame_length)/hop_length)
 
    vals = []
    freq = []
    time = []
    for i in range(frames_number):
        frame = y[int(i*hop_length):int(hop_length + frame_duration*(i+1))]
        val, freq = DFT(frame, frame_length, sr)
        vals.append(np.abs(val))
    time = np.arange(frames_number) * hop_length/sr
    vals = np.array(vals).T
    return vals, freq, time
    
    
 
vals, freq, time = Spectrogram(y, sr)
plt.pcolormesh(time, freq, 20*np.log10(vals), shading="gouraud")
plt.xlabel("Time")
plt.ylabel("Frequency")
plt.colorbar(label='Amplitude (dB)')
plt.show()

Vedi anche: Spettrogramma, DFT

Supponendo Di Avere Una Codifica DTMF Semplificata per Cui Il Simbolo 0 È Codificato Con Una Sinusoide a 700 Hz E Il Simbolo 1 È Codificato Con Una Sinusoide a 1200 Hz. Scrivere E Commentare Brevemente Il Codice Python Che Permetta Di Identificare Quale Dei due Simboli È Contenuto in Una Porzione Di Segnale Audio Caricata Da File, Eventualmente in Presenza Di Altri Rumori Di Disturbo.

import numpy as np
import librosa
import matplotlib.pyplot as plt
 
tonemap = {0: 700, 1: 1200}
 
# Genera Un Tono 0 O 1, Di Durata Duration E Frequenza Sr
def gen_tone(tone, duration, sr):
    t = np.linspace(0, duration, int(duration*sr), endpoint=False)
    return np.sin(2*np.pi*tonemap[tone]*t)
 
# Semplice DFT. Ritorna Sia Valori Che Frequenze.
def DFT(y, N, sr):
    val = np.fft.rfft(y, N)
    freq = np.fft.rfftfreq(N, d=1/sr)
    return val, freq
 
def filter(val, freq, centers=[700, 1200], threshold=5):
# Per Ogni Frequenza
    for i in range(len(val)):
        if not any(map(lambda x: abs(freq[i] - x) < threshold, centers)):
            val[i] = 0 # Azzera il valore se si trova più distante di 5 Hz da 700 o 1200
    return val, freq
 
def find_tone(val, freq):
# Prendi la Frequenza Associata Al Valore Massimo
    max = freq[np.argmax(val)]
# Prendi Il Valore Più Vicino Alla Frequenza Tra 700 E 1200 (potresti Fare Anche Un if < 1000 O > 1000)
    closest = min(tonemap.values(), key=lambda x:abs(x-max))
 
# Ritorna la Chiave Associata Alla Frequenza Trovata
    for key, value in tonemap.items():
        if value == closest:
            return key
 
sr = 44100
y = gen_tone(0, 1, sr)
 
# Mostra FT Attorno Alle Frequenze Dei Toni
val, freq = filter(*DFT(y, len(y), sr))
plt.plot(freq, np.abs(val))
plt.xlim(0, 1500)
plt.show()
 
print(find_tone(*filter(*DFT(y, len(y), sr))))

Scrivere E Commentare Brevemente Il Codice Python per Il Calcolo Del Cepstrum Di Un Frame Audio.

Scrivere E Commentare Brevemente Il Codice Python Che, in Base Al Modello Sorgente + Filtro, Utilizzi Le Funzioni Del modulo Python “signal” E la Funzione create_formant_filter (che Riceve Una Lista Con Le Frequenze Delle Prime Tre Formanti E Ritorna I Coefficienti B Ed a Del Filtro corrispondente) per Sintetizzare Il Suono Di Una Vocale Della Durata Di 2 Secondi, Frequenza Di Campionamento 16 kHz E Pitch 120 Hz.

Descrivere E Fornire Uno Schema, Utilizzando Il Formalismo Grafico Di Pure Data, Di Una Patch per la Sintesi FM Controllata Dai Seguenti Segnali: a) la Frequenza Portante, b) Rapporto M:C (o Harmonicity ratio), c) Indice Di Modulazione. (3 punti)

Descrivere E Fornire Uno Schema, Utilizzando Il Formalismo Grafico Di Pure Data, Di Una Patch per Realizzare Una Semplice Curva AR (attacco – Rilascio, Entrambi lineari) Che Moduli l’ampiezza Del Segnale Emesso Da Un Oscillatore Digitale. La Patch Deve Permettere Di Definire Il Valore Di Picco E Il Tempo Di Rilascio. (3 punti)