Quantizzazione

In elettronica e nell’analisi dei segnali, la quantizzazione è il processo di mappatura di valori di ingresso da un insieme grande (spesso continuo) a valori di uscita in un insieme più piccolo (numerabile), spesso con un numero finito di elementi. Esempi tipici di quantizzazione sono l’arrotondamento e il troncamento. La quantizzazione ha luogo in quasi ogni elaborazione di segnali digitali, dal momento che la rappresentazione di un segnale in forma digitale comporta effettuare arrotondamenti. Inoltre, la quantizzazione è al cuore di praticamente ogni algoritmo di compressione con perdita di informazioni.

Il processo non lineare di quantizzazione, a differenza di quello di campionamento (di un processo/segnale limitato), non è reversibile ovvero non è pertanto possibile ricostruire i valori reali assunti originariamente dalla grandezza fisica. La quantizzazione è dunque una fonte di distorsione.

Esistono due tipi di quantizzazione: mid-riser e mid-tread.

Mid-rise	Mid-tread
L’origine della funzione di quantizzazione si trova in mezzo ad un fronte di salita	L’origine della funzione di quantizzazione si trova in mezzo ad un segmento costante.

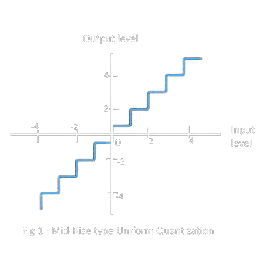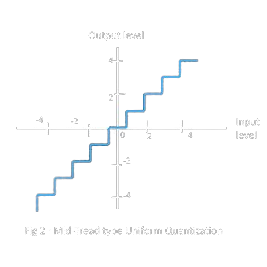Quindi il mid-tread permette di avere una quantizzazione che rappresenta anche il valore ZERO, mentre il mid-rise è simmetrico rispetto allo zero ma lo esclude. Si può quindi capire il tipo di rappresentazione digitale analizzando lo zero di un segnale.

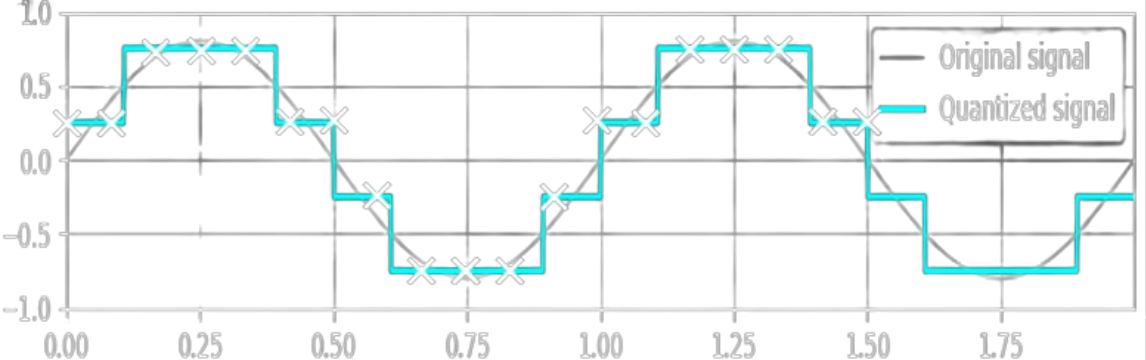
Ad esempio, in questo segnale lo zero non è mai rappresentato, quindi la rappresentazione è mid-rise.

def quantize_uniform(x, qmin=-1.0, qmax=1.0, qlevel=8):
	qstep = (qmax-qmin) / qlevel
	xnorm = (x-qmin) * qlevel / (qmax-qmin)
	xnorm[xnorm > qlevel] = qlevel
	xnorm[xnorm < 0] = 0
	xnorm_quant = np.floor(xnorm)
	xquant = xnorm_quant * (qmax-qmin) / qlevel
	xquant = xquant + qmin + qstep/2
	return xquant

Quando si quantizza un segnale è importante adattare il quantizzatore in modo tale da far prendere al segnale buona parte del range del segnale quantizzato.

Avere un segnale di ampiezza $\pm 1$ con un quantizzatore da 3 bit con ampiezza $\pm 3$ è poco efficace perché i valori generati dal quantizzatore sono [-3.0, -2.25, -1.5, -0.75, 0.75, 1.5, 2.25, 3.0], quindi il segnale di ingresso userà soltanto due di questi valori (-0.75 e 0.75).

Se invece adattassimo il quantizzatore al segnale con un’ampiezza di $\pm 1.0$ si ottiene che i valori generati sono [-1.0, -0.75, -0.5, -0.25, 0.25, 0.5, 0.75, 1.0] e quindi tutti gli otto valori vengono utilizzati.

L’SNR del primo caso è 35.37, mentre nel secondo caso è 3.85, quindi adattare il quantizzatore è importante anche per aumentare la qualità della quantizzazione.